(c) \(\frac{\pi}{2}\)

Let PQ be the vertical pole of height h.
If the angle of elevation of the sun’s ray is α, then the length of the shadow QR = h cot α
In ΔQRP, for the first moment, we take α = α1
Given, h cot α1 = h ⇒ cot α1 = 1 ⇒ tan α1 = 1
For the second moment, α = α2 (say)
Given, h cot α2 = 2h ⇒ tan α2 = \(\frac{1}{2}\)
Now, for the third moment, α = α3 (say)
h cot α3 = 3h ⇒ tan α3 = \(\frac{1}{3}\)
Now, we need to find the value of α1 + α2 + α3. tan (α1 + α2 + α3)
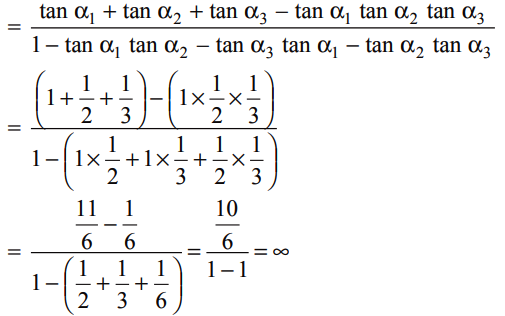
tan (α1 + α2 + α3) = tan \(\frac{\pi}{2}\) ⇒ α1 + α2 + α3 = \(\frac{\pi}{2}\).