Given: m∠ PQR = 105° and m∠ QRP = 40°
Therefore m∠ PQR + m∠ QRP + m∠ QPR = 180°
⇒ 105° + 40° + m∠ QPR = 180°
⇒ 145° + m∠ QPR = 180°
⇒ m∠QPR = 180° – 145°
⇒ m∠ QPR = 35°
To construct: Δ PQR where m∠ P = 35° , m∠ Q = 105° and PQ = 5 cm.
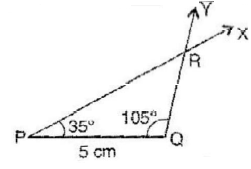
Steps of construction:
(a) Draw a line segment PQ = 5 cm.
(b) At point P, draw ∠ XPQ = 35° with the help of protractor.
(c) At point Q, draw ∠ YQP = 105° with the help of protractor.
(d) XP and YQ intersect at point R.
It is the required triangle PQR.