Given In a parallelogram ABCD, P and Q are the mid-points of AB and CD, respectively.
To show PRQS is a parallelogram.
Proof Since, ABCD is a parallelogram.
`" "AB||CD" "`
`rArr" "AP||QC`
Also, `" "AB=DC`
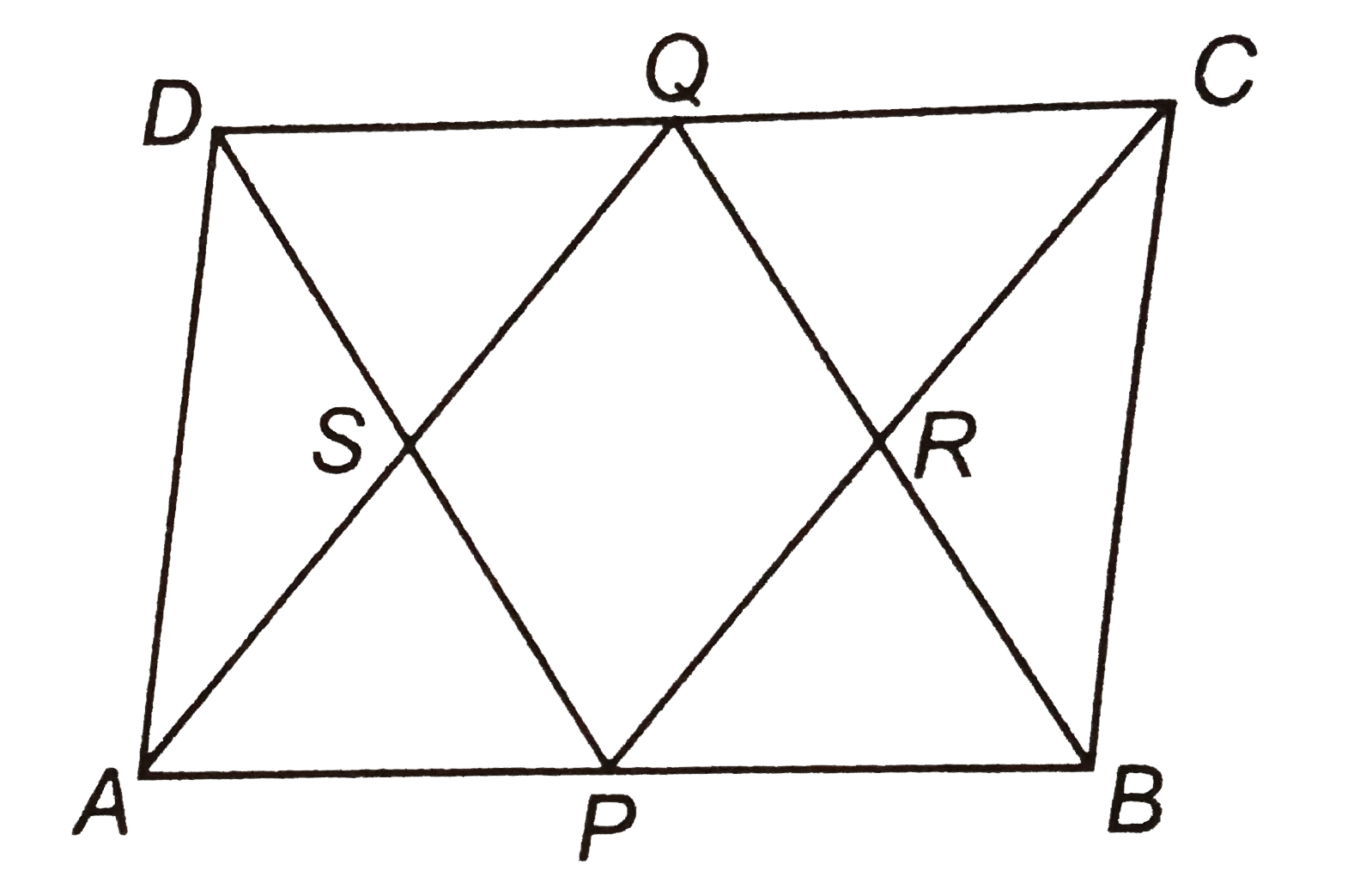
`" "(1)/(2)AB=(1)/(2)DC" "` [dividing both sides by 2]
`rArr" "AP=QC" "` [ since, P and Q are the mid-points of AB and DC]
Now, `" "AP||QC and AP=QC`
Thus APCQ is a parallelogram.
`therefore" "AQ||PC or SQ||PR" "...(i)`
Again, `" "AB||DC or BP||DQ`
Also, `" "AB=DC rArr(1)/(2)AB=(1)/(2)DC" "` [dividing both sides by 2]
`rArr" "BP=QD` [since, P and Q are the mid-points of AB anc DC]
Now, `" "BP||QD and BP=QD`
So, BPDQ is a parallelogram.
`therefore" "PD||BQ or PS||QS" "...(iii)`
From Eqs. (i) and (ii), `" "SQ||RQ and PS||QR`
So, PRQS is a parallelogram. `" "` Hence proved.