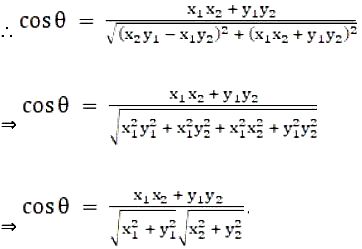Question

If θ is the angle which the straight line joining the points (x₁, y₁) and (x₂, y₂) subtends at the origin, prove that tanθ =  \(\frac{x_2y_1 - x_1y_2}{x_1x_2 + y_1y_2}\)  and cos θ = \(\frac{x_1x_2 + y_1y_2 }{\sqrt{x_1^2 + y_1^2 }\sqrt{x_2^2 + y^2_2}}\)

Answer 1

To prove:

tan θ =  \(\frac{x_2y_1 - x_1y_2}{x_1x_2 + y_1y_2}\) and cos θ = \(\frac{x_1x_2 + y_1y_2 }{\sqrt{x_1^2 + y_1^2 }\sqrt{x_2^2 + y^2_2}}\)

Assuming: 

A (x₁, y₁) and B (x₂, y₂) be the given points and O be the origin. 

Explanation:

Slope of OA = m₁ = y₁x₁ 

Slope of OB = m₂ = y₂x₂ 

It is given that θ is the angle between lines OA and OB.

Now, As we know that cos θ = \(\sqrt{\frac{1}{1+ tan^2θ}}\)