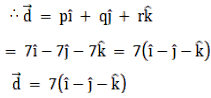Question

Let vectors a = 4i + 5j - k, b = i - 4j + 5k and c = 3i + j - k. Find a vector d which is perpendicular to both a and b and is such that d. c = 21.

Answer 1

 \(\vec{a} =( \vec{4i} + \vec{5j} - \vec{k})\)

\(\vec{b} = (\vec{i} - \vec{4j} + \vec{5k})\)

 \(\vec{c} = (\vec{3i} + \vec{j} - \vec{k})\) 

Let   \(\vec{d} = \vec{pi} + \vec{qj} - \vec{rk}\) 

the vector \(\vec{d}\) which is perpendicular to both \(\vec{a}\) and \(\vec{b}\)

Solving equations 1,2,3 simultaneously we get

p = 7,q = - 7,r = - 7