Given : ABCD is a rhombus in which P, Q, R and S are mid points of sides AB, BC, CD and DA respectively :
To Prove : PQRS is a rectangle.
Construction : Join AC, PR and SQ.
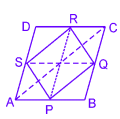
Proof : In ∆ABC
P is mid point of AB [Given]
Q is mid point of BC [Given]
⇒ PQ || AC and PQ = 1/ 2 AC …(i) [Mid point theorem]
Similarly, in ∆DAC,
SR || AC and SR = 1 2 AC …(ii)
From (i) and (ii), we have PQ||SR and PQ = SR
⇒ PQRS is a parallelogram [One pair of opposite sides is parallel and equal]
Since ABQS is a parallelogram
⇒ AB = SQ [Opposite sides of a || gm]
Similarly, since PBCR is a parallelogram.
⇒ BC = PR
Thus, SQ = PR [AB = BC]
Since SQ and PR are diagonals of parallelogram PQRS, which are equal.
⇒ PQRS is a rectangle. Proved.