Given : A trapezium ABCD in which AB || CD and AD = BC.
To Prove : ABCD is a cyclic trapezium.
Construction : Draw DE ⊥ AB and CF ⊥ AB.
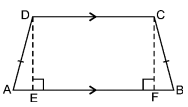
Proof : In ∆DEA and ∆CFB, we have
AD = BC [Given]
∠DEA = ∠CFB = 90° [DE ⊥ AB and CF ⊥ AB]
DE = CF
[Distance between parallel lines remains constant]
∴ ∆DEA ≅ ∆CFB [RHS axiom]
⇒ ∠A = ∠B ...(i) [CPCT]
and, ∠ADE = ∠BCF ..(ii) [CPCT]
Since, ∠ADE = ∠BCF [From (ii)]
⇒ ∠ADE + 90° = ∠BCF + 90°
⇒ ∠ADE + ∠CDE = ∠BCF + ∠DCF
⇒ ∠D = ∠C ..(iii)
[∠ADE + ∠CDE = ∠D, ∠BCF + ∠DCF = ∠C]
∴ ∠A = ∠B and ∠C = ∠D [From (i) and (iii)] (iv)
∠A + ∠B + ∠C + ∠D = 360° [Sum of the angles of a quadrilateral is 360°]
⇒ 2(∠B + ∠D) = 360° [Using (iv)]
⇒ ∠B + ∠D = 180°
⇒ Sum of a pair of opposite angles of quadrilateral ABCD is 180°.
⇒ ABCD is a cyclic trapezium Proved