Question

Radha made a picture of an aeroplane with coloured paper as shown in the figure. Find the total area of the paper used.

Answer 1

For the triangle marked I : a = 5 cm, b = 5 cm, c = 1 cm 

∴ s = (a +b + c)/ 2 =  (5 +5+ 1) /2 cm =  11 / 2 cm  =5.5 cm 

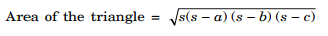
For the rectangle marked II : 

Length = 6.5 cm, Breadth = 1 cm 

Area of the rectangle = 6.5 × 1 cm² = 6.5 cm² 

For the trapezium marked III : 

Draw AF || DC and AE ⊥ BC. 

AD = FC = 1 cm, DC = AF = 1 cm 

∴ BF = BC – FC = (2 – 1) cm = 1 cm 

Hence, ∆ABF is equilateral. 

Also, E is the mid-point of BF. 

∴ BE = 1/ 2 cm = 0.5 cm 

Also, AB² = AE² + BE² [Pythagoras theorem] 

⇒ AE² = 1² – (0.5)² = 0.75 

⇒ AE = 0.9 cm (approx.) 

Area of the trapezium = 1/ 2 (sum of the parallel sides) × distance between them. 

= 1/ 2 × (BC + AD) × AE = 1/ 2 × (2 + 1) × 0.9 cm² = 1.4 cm². 

For the triangle marked IV : 

It is a right-triangle 

∴ Area of the triangle = 1/ 2 × base × height 

= 1/ 2 × 6 × 1.5 cm cm² = 4.5 cm². 

For the triangle marked V : 

This triangle is congruent to the triangle marked IV. 

Hence, area of the triangle = 4.5 cm² 

Total area of the paper used = (2.5 + 6.5 + 1.4 + 4.5 + 4.5) cm²