Question

A car, starting from rest, accelerates at the rate (f) through a distance (S), then continues at constant speed for some time (t) and then decelerates at the rate ` f//2` to come to rest. If the total distance is ` 5 S`, then prove that
` S=1/2/ ft^(2)`.
A. ` S = (1)/(6) ft^(2)`
B. ` S = ft`
C. ` s = (1)/(4) ft^(2)`
D. ` s = (1)/(72) ft^(2)`

Answer 1

Correct Answer - D
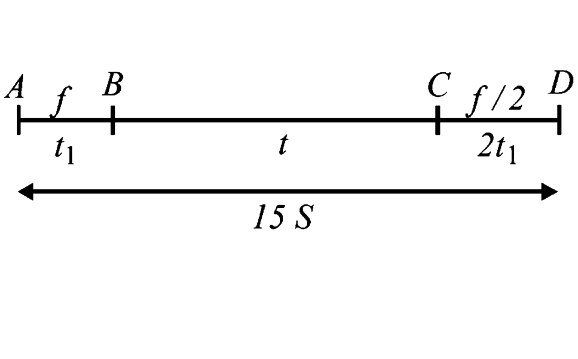
Distance from `A to B = S = (1)/(2) ft_(1)^(2) rArr ft_(1)^(2) rArr ft_(1)^(2) = 2S `
Distance from ` B to C = (f_(1))t `
Distance from `C to D = (u^(2))/(2a) = ((ft_(1))^(2))/2(f//2) = ft_(1)^(2) = 2S`
`rArr S + f t_(1)t + 2 S = 15 S rArr f t_(1)t = 12 S `
But `1/2 f t_(1)^(2) = S `
On dividing the above two equations , we get `t_(1) = (t)/(6) `
`rArr S = 1/2 f (t/6)^(2) = (f t^(2))/(72) `