Application of Integral Formula class 12

Question

Learn all Application of Integral Formula class 12 for better understanding of concept and solve numerical questions easily.

Answer 1

Application of integrals:

At this stage, you must be aware of every formula to calculate areas of simple geometrical figures which includes Triangles, Rectangles, trapeziums and circles. For the calculation of areas of such simple figures, we use formulae of elementary geometry. Why do we need to study application of integral formula?

Also, ever you thought that the figures which are not included in elementary geometry say, curves. How to calculate areas of such figures?

Now, we understood that area for elementary geometry is inadequate for calculating the areas enclosed by curves. For calculating the area under curves we need some concepts of Integral Calculus. We need application of integrals to find the area under simple curves, area between lines and arcs of circles, parabolas and ellipses (standard forms only).

Special Terminology:

Elementary strip: In a simple curve we can think of area under the curve as composed of large number of very thin vertical strips. Consider an arbitrary strip of height y and width dx, then dA (area of the elementary strip)= ydx, where, y = f(x).

Application of Integral Formula:

Area bounded by curve and lines:

1. The area of the region bounded by the curve y = f (x), x-axis and the lines x = a and x = b where (b > a) is given by the application of integral formula as:
   \(\LARGE Area = \int_{a}^{b}ydx = \int_{a}^{b}f(x)dx\)
2. The area of the region bounded by the curve x = φ (y), y-axis and the lines y = c, y = d is given by the application of integral formula as:
   \(\LARGE Area = \int_{c}^{d}xdy = \int_{c}^{d}φ(y)dy\)

3.       The area of the region enclosed between two curves y = f (x), y = g (x) and the lines x = a, x = b is given by the application of integral formula as:
\(Area = \int\limits_{a}^b  [f(x) – g(x)] dx\)
where, f (x) ≥ g (x) in [a, b]4.       If f (x) ≥ g (x) in [a, c] and f (x) ≤ g (x) in [c, b], a < c < b, then
\(Area = \int\limits_{a}^c  [f(x) – g(x)] dx + \int\limits_{c}^b [g(x) – f(x)] dx \)

Application of Integral Formula Examples:

1. Find the area of the region bounded by the two parabolas y = x² and y² = x.
   Solution:
   
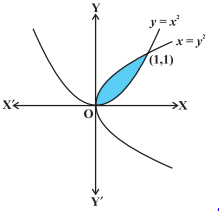
   The point of intersection of these two parabolas are O (0, 0) and A (1, 1) as in the figure:
   Here, we stay as y ² = x or y = \(\sqrt{x}\) = f(x) and y = x² = g (x), where, f (x) ≥ g (x) in [0, 1].
   So, the required area of the shaded region is:
   \(A = \int\limits_{0}^1 [f(x) – g(x)] dx\)
   \(\int\limits_{0}^1  [\sqrt{x}– {x}^2] dx\) = \([\frac{2}{3}\:x^{\frac{3}{2}} - \frac{{x}^3}{3}{]}_{0}^{1}\)
    = \(\frac{2}{3}- \frac{1}{3} = \frac{1}{3}\) sq.units
2. Find the area of the parabola y² = 4ax bounded by its latus rectum.
   Solution:
   
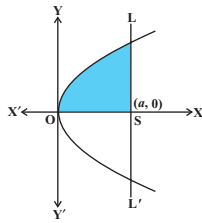
   From the figure, we see that equation of the latus rectum LSL′ is x = a. Also, parabola is symmetrical about the x-axis.
   The required area of the region OLL′O = 2 (area of the region OLSO)
   = 2 \(\int\limits_{0}^a y.dx\) = 2 \(\int\limits_{0}^a \sqrt{4ax}.dx\)
   = 4\(\sqrt{a}\) \(\int\limits_{0}^a \sqrt{x}.dx\)
   = \(\frac{8}{3}\) a²