Question

Electricity – Ohm’s Law, Potential Difference, Heating Effect Notes Class 10 for Revision

Answer 1

Electricity:

In the modern world we see each section of the society is dependent on electricity in either way. From small household to big industries each has a major dependency on it. Have you ever thought that what electricity is actually made up of? In this article we will discuss everything related to electricity.

Charge:

• Charge is a basic property of matter which is responsible for all electric and magnetic interactions.
• It is the fundamental particle of an atom.
• There are two types of charge, positive charge and negative charge.
• Like charges repel each other while unlike charges attract each other.
• The SI unit of charge is coulomb.
• 1 coulomb charge is the sum of charges present on 6 x 10⁸
• An electron possesses a negative charge of 6 × 10^–19 C.

Electric Current:

• The amount of flow of electric charge through a particular area in unit time is called electric current. (Simply, The rate of flow of charge is electricity).
• Electrons constitute the flow of charges.
• Before the discovery of electrons electric current was said to be as the flow of positive charges.
• Conventionally, in an electric circuit the direction of electric current is taken as opposite to the direction of the flow of electrons.
• If Q charge flows across any cross-section of a conductor in time t, then current I, passing through the cross-section is
  I = \(\frac{Q}{t}\)
• The unit of electric current is ampere.
• 1 Ampere current may be defined as the flow of one coulomb of charge per second.
• Ammeter is the device which is used to measure electric current in a circuit and is always connected in series with the circuit.

Value Conversion
1Ampere (A)	1 C/s
1 Mili-ampere(mA)	10-3 A
1 Micro-ampere(μA)	10-6 A

Electric circuit:

• A continuous and closed path of an electric current is called electric circuit.
• If the circuit is broken anywhere the current stops flowing.
• Electricity flows in the circuit from the positive terminal of the cell to the negative terminal of the cell.

Electric Potential:

• The amount of work done in bringing a unit positive charge from infinity to a point is said to be potential of the point.
• The unit of electric potential is Volt.
• Positive charge move from Higher potential to Lower potential whereas electrons (negative charge) moves from Lower to Higher potential.

Potential Difference:

• The amount of work done in bringing a unit positive charge from one point to another point is said to be potential difference between the points.
• For flow of charges, the electrons move only if there is a difference of electric pressure.
• Potential difference is created by cell or a battery by chemical action within them. thus, cause the flow of electricity.
• Potential difference (V) between two points = \(\frac{Work\:done\:(W)}{Charge\:(Q)}\)

V = \(\frac{W}{Q}\)

• The SI unit of electric potential difference is volt (V).
• One volt potential difference may be defined as potential difference between two points in a current carrying conductor when 1 joule of work is done to move a charge of 1 coulomb from one point to the other.

1 volt = \(\frac{1\:joule}{1\:coulomb}\) = 1 J/C

• Voltmeter is the instrument which is used to measure the potential difference. It is always connected in parallel with the device of which the potential difference is calculated.

Circuit Diagram:

• An electric circuit contains comprises a cell (or a battery), connecting wires, plug key and electrical component(s).
• We often draw a schematic diagram in which the symbols of the respective components are used.
• The important conventional symbols of some circuit elements are listed here.

Ohm’s law:

• Voltage, current and resistance are the main components of electricity.
• These quantities are related to each other by a law called Ohm’s law.
• According to Ohm’s law “The current passing through a circuit is directly proportional to the potential difference across its end points.”
• Ohm’s law in electricity is valid only when temperature remains constant.

• Electric Current ∝ Potential difference
  i ∝ V
  i = \(\frac{V}{R}\)
  V = iR

• Here R is constant for the given conductor and is called resistance.

Answer 2

Resistance:

• Resistance is the property of a conductor by which it opposes the flow of electric current through it.

R = \(\frac{V}{I}\)

• The SI unit of Resistance is ohm (Ω).
• 1 ohm is the resistance when potential difference across conductor is 1 V and the current through it is 1 ampere.
• The electrical appliance which is used to oppose the current flow in a circuit is called resistor.
• Variable resistance (Rheostat) is the component used to regulate current (electricity) without changing the voltage source.

Factors affecting resistance:

Factors on which the resistance of a conductor depends are:

1. Length of conductor (R ∝ l)
2. Area of cross section (R ∝ \(\frac{1}{A}\) )
3. Nature of material
4. Temperature

Resistivity:

• Resistance of a uniform metallic conductor is directly proportional to its length (l) and inversely proportional to the area of cross-section (A).
• R ∝ l
  R ∝ \(\frac{1}{A}\)
  Thus,
  R ∝ \(\frac{1}{A}\)

R = ρ \(\frac{l}{A}\)

• Here, ρ (rho) is a constant of proportionality and is called the electrical resistivity.
• The SI unit of resistivity is Ω m.
• Resistivity is characteristic property of the material.
• Resistance, as well as resistivity both, varies with change in temperature.

Resistivity chart:

Elements	Conductivity	Resistivity range
Metals and alloys	Good conductors	10–8 Ω m to 10–6 Ω m.
Rubber, glass	Insulators	1012 Ω m to 1017 Ω m.

Combination of resistors:

There are two systems of combination of resistors. They are:

1. Series combination
2. Parallel combination

Resistance in series:

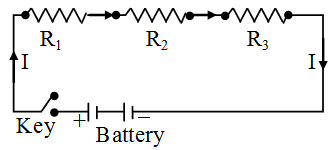
• When two or more resistors is joined end to end between two given points in a circuit, then these combination is said to be in series combination.
• Same current flows throughout the circuit i.e. same current flows through each resistor.
• Potential difference will be the sum of individual potential differences across each resistors.
• Ohm’s law can be applied to the combination to get equivalent resistance.

Equivalent resistance (R_s) in series combination:

V = V₁ + V₂ + V₃
Now, we apply Ohm’s law:
iR_s = iR₁ + iR₂ + iR₃
R_s = R₁ + R₂ + R₃

• We conclude that equivalent resistance in series combination is obtained by adding each individual resistance.
• Equivalent resistance is always greater than each individual resistance in series combination.

Resistance in Parallel:

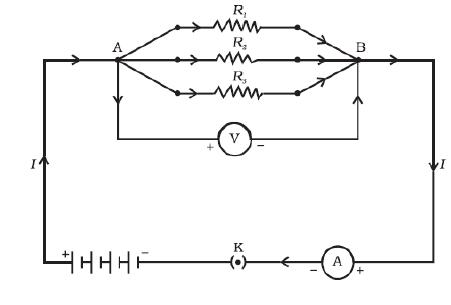
• When ends of two or more resistors are joined to the two given point in a circuit, then these combination is called parallel combination.
• Potential difference between the two points across resistors are same.
• There will be different current flowing through each resistors.

Equivalent resistance (R_p) in series combination:

I = I₁ + I₂ + I₃
By applying Ohm’s law:
\(\frac{V}{R_P}\) = \(\frac{V}{R_1}\) + \(\frac{V}{R_2}\) + \(\frac{V}{R_3}\)

\(\frac{1}{R_P}\) = \(\frac{1}{R_1}\) + \(\frac{1}{R_2}\) + \(\frac{1}{R_3}\)

• Thus, equivalent resistance across parallel combination of resistors is the sum of reciprocal of each individual resistance.
• The equivalent resistance of resistors in parallel combination is always less then the individual resistances.

Advantage of Parallel combination:

• In series combination a low and a high resistance can’t work properly, as current in series is same throughout. But current needed in each resistor is different. Whereas in parallel combination they work properly.
• In series combination, when one component fails the circuit is broken and none of the components works on the other hand there is no effect of failure of one component on other in parallel combination.

Heating Effect of Electric Current:

• If electric circuit is purely resistive then energy continually gets dissipated entirely in the form of heat. This is said to be heating effect of electric current.
• If I is current, R is resistance, V is potential difference, then work done in moving the charge Q through a potential difference V is VQ.
• The rate of consumption or dissipation of energy in an electric circuit is called electric power.
• Power = \(\frac{work \:done}{time}\) = \(\frac{VQ}{t}\) = V\(\frac{Q}{t}\) = VI
• Energy supplied to the circuit in time t = P x t = Heat produced

Thus, Heat produced (H) = VIt = I²Rt

Joule’s law of heating:

According to Joule’s law of heating:

1. For a given resistance, the heat produced in a resistor is directly proportional to the square of current.
   e. H ∝ i²
2. For a given current, the heat produced in a resistor is directly proportional to resistance.
   e. H ∝ R
3. The heat produced directly proportional to the time for which the current flows through the resistor.
   e. H ∝ t

Electric bulb:

• This is said to be the best discovery which uses electricity.
• The filament of electric bulb is made up of tungsten.
• Tungsten has very high melting point (3380⁰C).
• The bulbs are usually filled with chemically inactive nitrogen and argon gases to prolong the life of filament.

Electric power:

• The rate at which electrical energy is consumed or dissipated in an electric circuit is known as electric power.

P = VI = I²R = V²/R

• The SI unit of electric power is watt (W).
• 1 watt is the power consumed by an appliance that carries 1 A of current when operated at a potential difference of 1 V.

1 W = 1 volt × 1 ampere = 1 V A

• On large scale we measure electricity or electric power as kilowatt (1000 watt). Energy is counted in P x t so the unit we use to measure energy consumption commercially in KW h.