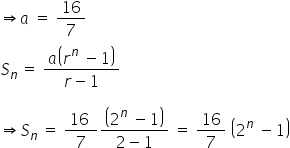Solution:
Let the G.P. be a, ar, ar2, ar3, …
According to the given condition,
a + ar + ar2 = 16 and ar3 + ar4 + ar5 = 128
⇒ a (1 + r + r2) = 16 … (1)
ar3(1 + r + r2) = 128 … (2)
Dividing equation (2) by (1), we obtain

Substituting r = 2 in (1), we obtain
a (1 + 2 + 4) = 16
⇒ a (7) = 16