Find four numbers forming a geometric progression in which the third term is > the first term by 9, and the second term is > the 4th by 18.

Question

Find four numbers forming a geometric progression in which the third term is greater than the first term by 9, and the second term is greater than the 4th by 18.

Answer 1

Let a be the first term and r be the common ratio of the G.P.

a₁ = a, a₂ = ar, a₃ = ar², a₄ = ar³

By the given condition,

a₃ = a₁ + 9

⇒ ar² = a + 9 … (1)

a₂ = a₄ + 18

⇒ ar = ar³ + 18 … (2)

From (1) and (2), we obtain

a(r² ­­– 1) = 9 … (3)

ar (1– r²) = 18 … (4)

Dividing (4) by (3), we obtain

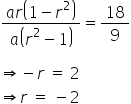
Substituting the value of r in (1), we obtain

4a = a + 9

⇒ 3a = 9

∴ a = 3

Thus, the first four numbers of the G.P. are 3, 3(– 2), 3(–2)², and 3­(–2)³ i.e., 3¸–6, 12, and –24.