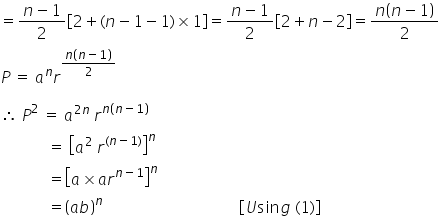Solution:
The first term of the G.P is a and the last term is b.
Therefore, the G.P. is a, ar, ar2, ar3, … arn–1, where r is the common ratio.
b = arn–1 … (1)
P = Product of n terms
= (a) (ar) (ar2) … (arn–1)
= (a × a ×…a) (r × r2 × …rn–1)
= an r 1 + 2 +…(n–1) … (2)
Here, 1, 2, …(n – 1) is an A.P.
∴1 + 2 + ……….+ (n – 1)