Correct option is (D) All of these
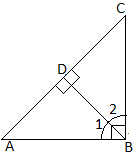
Given that \(\angle B=90^\circ\) & \(BD\bot AC\)
\(\therefore\) \(\angle A+\angle B+\angle C=180^\circ\) (In \(\triangle ABC)\)
\(\Rightarrow\) \(\angle A+\angle C=90^\circ\) _______________(1) \((\because\angle B=90^\circ)\)
Let \(\angle ABD=\angle 1\;\&\;\angle CBD=\angle 2\)
In \(\triangle ADB,\)
\(\angle A+\angle ADB+\angle 1=180^\circ\)
\(\Rightarrow\) \(\angle A+\angle 1=90^\circ\) _______________(2) \((\because\angle ADB=90^\circ\,as\,BD\bot AC)\)
From (1) & (2), we obtain
\(\angle C=\angle1\) _______________(3)
(A) In right \(\triangle ADB\;\&\;\triangle BDC,\)
\(\angle C=\angle1\) (From (3))
\(\angle ADB=\angle BDC=90^\circ\) \((BD\bot AC)\)
\(\therefore\) \(\triangle ADB\sim\triangle BDC\) (By AA similarity rule)
(B) In right \(\triangle ADB\;\&\;\triangle ABC,\)
\(\angle DAB=\angle BAC\) (Common angle)
\(\angle ADB=\angle ABC=90^\circ\) (Given)
\(\therefore\) \(\triangle ADB\sim\triangle ABC\) (By AA similarity rule)
(C) \(\because\) \(\triangle ADB\sim\triangle BDC\) & \(\triangle ADB\sim\triangle ABC\)
\(\therefore\) \(\triangle BDC\sim\triangle ABC\)