​ Area of a triangle enclosed by the axes and the line x/a + y/b = 1 is a b ​

Question

Area of a triangle enclosed by the axes and the line \(\cfrac{x}a\) + \(\cfrac{y}b\) = 1 is a b

A) \(\cfrac{ab}3\)

B) \(\cfrac{a^2b^2}2\)

C) \(\cfrac{ab}2\)

D) \(\cfrac{a+b}2\)

Answer 1

Correct option is (C) \(\frac{ab}{2}\)

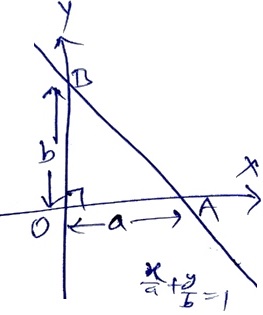
Given line is \(\frac{x}{a} + \frac{y}{b} =1\)

\(\therefore\) x-intercept of line is a & y-intercept of line is b.

Since, both coordinate is perpendicular to each other.

\(\therefore\) Triangle formed by line \(\frac{x}{a} + \frac{y}{b} =1\) & coordinate axes  is a right angled triangle.

In right \(\triangle OAB,\)

OA = x-intercept of line = a,

OB = y-intercept of line = b

\(\therefore\) Area of triangle \(\triangle AOB\) \(=\frac12\times OA\times OB\)

\(=\frac12ab\) square units

Hence, area of triangle enclosed by the axes & the line \(\frac{x}{a} + \frac{y}{b} =1\) is \(\frac{ab}{2}\) square units.

Answer 2

Correct option is C) \(\cfrac{ab}2\)