Solution:
(i) Let the breadth = x metres
Length = 2 (Breadth) + 1
Length = (2x + 1) metres
Since Length × Breadth = Area
∴ (2x + 1) × x = 528
2x2 + x = 528
2x2 + x – 528 = 0
Thus, the required quadratic equation is
2x2 + x – 528 = 0
(ii) Let the two consecutive numbers be x and (x + 1).
∵ Product of the numbers = 306
∴ x (x + 1) = 306
⇒ x2 + x = 306
⇒ x2 + x – 306 = 0
Thus, the required equdratic equation is
x2 + x – 306 = 0
(iii) Let the present age = x
∴ Mother’s age = (x + 26) years
After 3 years
His age = (x + 3) years
Mother’s age = [(x + 26) + 3] years
= (x + 29) years
According to the condition,

⇒ (x + 3) × (x + 29) = 360
⇒ x2 + 29x + 3x + 87 = 360
⇒ x2 + 29x + 3x + 87 – 360 = 0
⇒ x2 + 32x – 273 = 0
Thus, the required quadratic equation is
x2 + 32x – 273 = 0
(iv) Let the speed of the tram = u km/hr
Distance covered = 480 km
Time taken = Distance + Speed
= (480 ÷ u) hours
= 480/u hours
In second case,
Speed = (u – 8) km/ hour

According to the condition,
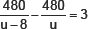
⇒ 480u – 480(u – 8) = 3u(u – 8)
⇒ 480u – 480u + 3840 = 3u2 – 24u
⇒ 3840 – 3u2 + 24u = 0
⇒ 1280 – u2 + 8u = 0
⇒ –1280 + u2 – 8u = 0
⇒ u2 – 8u – 1280 = 0
Thus, the required quadratic equation is
u2 – 8u – 1280 = 0