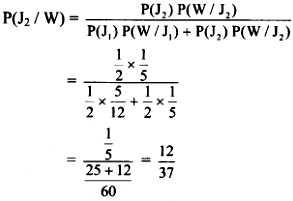Let event J1 : Ball drawn from jar I,
event J2 : Ball drawn from jar II.
P(J1) = P(head) = 1/2
P(J2) = P(tail) = 1/2
Let event W: Ball drawn is white.
In Jar I, there are total 12 balls, out of which 5 balls are white.
∴ Probability that the ball drawn is white under the condition that it is drawn from Jar I.
P(W/J1) = \(\frac {^5C_1}{^{12}C_1} = \frac {5} {12}\)
Similarly, P(W/J2) = \(\frac {^3C_1}{^{15}C_1} = \frac {3} {15} = \frac 1 5\)
Required probability = P(J2/W)
By Bayes’ theorem