Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:

Question

(i) (– 1, – 2), (1, 0), (– 1, 2), (– 3, 0)
(ii) (–3, 5), (3, 1), (0, 3), (–1, – 4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)

Answer 1

Let the points ( - 1, - 2), (1, 0), ( - 1, 2), and ( - 3, 0) be representing the vertices A, B, C, and D of the given quadrilateral respectively.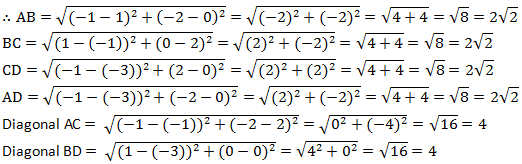
It can be observed that all sides of this quadrilateral are of the same length and also, the diagonals are of the same length. Therefore, the given points are the vertices of a square.

(ii) Let the points ( - 3, 5), (3, 1), (0, 3), and ( - 1, - 4) be representing the vertices A, B, C, and D of the given quadrilateral respectively.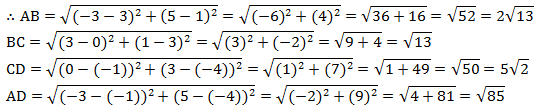
It can be observed that all sides of this quadrilateral are of different lengths. Therefore, it can be said that it is only a general quadrilateral, and not specific such as square, rectangle, etc.

(iii) Let the points (4, 5), (7, 6), (4, 3), and (1, 2) be representing the vertices A, B, C, and D of the given quadrilateral respectively.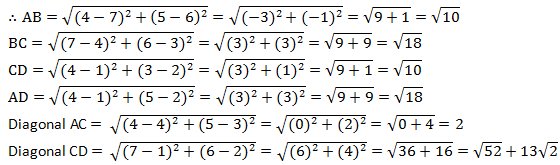
It can be observed that opposite sides of this quadrilateral are of the same length. However, the diagonals are of different lengths. Therefore, the given points are the vertices of a parallelogram.