Let the resistance of the electric lamp be Rlamp.
Current (I) = 1 A
Resistance of conductor (Rconductor) = 5Ω
Potential difference of battery (V) = 10 V

Since the lamp and the conductor is connected in series, thus same current 1 A will pass through both of them.
Using Ohm's law,
Rnet = \(\frac VI\)
Rnet = \(\frac{10}1\)
Rnet = 10Ω
Rnet = Rlamp + Rconductor
⇒ 10 = Rlamp + 5
⇒ Rlamp = 5Ω
Potential difference across lamp,
Vlamp = I × Rlamp = 1 × 5 = 5V
When 10Ω resistor is connected parallel to the series combination of lamp and conductor (Rnet = 5 + 5 = 10Ω) then the equivalent resistance,
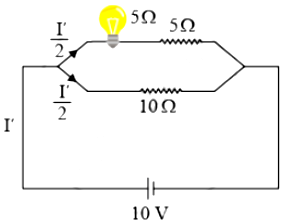
\(\frac 1{R_{eq}} = \frac 1{10} + \frac 1{10} \)
\(= \frac 2{10}\)
\(= \frac 15\)
⇒ Req = 5Ω
Using Ohm's law,
\(I' = \frac V{R_{eq}}\)
⇒ \(I' = \frac{10}5\)
⇒ \(I' = 2A\)
Current will distribute equally in two parallel parts.
Thus,\(\frac{I'}2 = 1A\) current will pass through both the lamp and the resistor of 5Ω (because they are connected in series).
Potential difference across the lamp (Rlamp) = 5Ω
V'lamp = 1 × 5 = 5V
Hence, there will be no change in current through the conductor of resistance 5Ω, and potential difference across the lamp.