Solution:
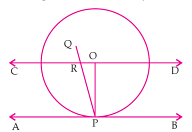
Let AB be the tangent to the circle at point P with centre O.
We have to prove that PQ passes through the point O.
Suppose that PQ doesn't passes through point O. Join OP.
Through O, draw a straight line CD parallel to the tangent AB.
PQ intersect CD at R and also intersect AB at P.
AS, CD || AB PQ is the line of intersection,
∠ORP = ∠RPA (Alternate interior angles)
but also,
∠RPA = 90° (PQ ⊥ AB)
⇒ ∠ORP = 90°
∠ROP + ∠OPA = 180° (Co-interior angles)
⇒∠ROP + 90° = 180°
⇒∠ROP = 90°
Thus, the ΔORP has 2 right angles i.e. ∠ORP and ∠ROP which is not possible.
Hence, our supposition is wrong.
∴ PQ passes through the point O.