Solution:
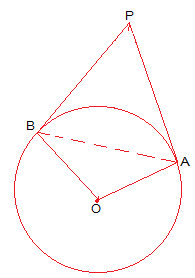
Consider a circle with centre O. Let P be an external point from which two tangents PA and PB are drawn to the circle which are touching the circle at point A and B respectively and AB is the line segment, joining point of contacts A and B together such that it subtends ∠AOB at center O of the circle.
It can be observed that
OA ⊥ PA
∴ ∠OAP = 90°
Similarly, OB ⊥ PB
∴ ∠OBP = 90°
In quadrilateral OAPB,
Sum of all interior angles = 360º
∠OAP +∠APB +∠PBO +∠BOA = 360º
⇒ 90º + ∠APB + 90º + ∠BOA = 360º
⇒ ∠APB + ∠BOA = 180º
∴ The angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.