10. How many 176 Ω resistors (in parallel) are required to carry 5 A on a 220 V line?
Answer:
Let the total number of resistors be x.
Given that:
Current I = 5 A and Potential Difference V = 220 V
According to Ohm’s law, V = IR
⇒ R = \(\frac{V}{I}=\frac{220}5\) = 44 \(\Omega\)
Now for x number of resistors of resistance 176 \(\Omega\), the equivalent resistance of the resistors connected in parallel is 44 \(\Omega\).
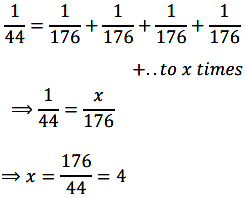
Therefore, 4 resistors of 176 \(\Omega\) are required to draw the given amount of current.
11. Show how you would connect three resistors, each of resistance 6 Ω, so that the combination has a resistance of (i) 9 Ω, (ii) 4 Ω.
Answer:
(i). To get total 9 Ω resistance from three 6 Ω resistors, we should connect two resistors in parallel and the third resistor in series with the resultant. The combination is given as follows:

Total resistance in parallel is given by
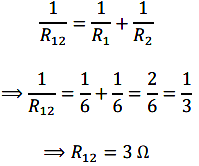
Now R12 and 6 \(\Omega\) are connected in series, so the net resistance is given by
R = R12 + 6 \(\Omega\) = 3 \(\Omega\) + 6 \(\Omega\) = 9 \(\Omega\)
(ii). To get total 4\(\Omega\) resistance from three 6\(\Omega\) resistors, we should connect two resistors in series and the third resistor in parallel with the resultant. The combination is given as follows:

Total resistance in series is given by
R12 = R1 + R2 = 6 \(\Omega\) + 6 \(\Omega\) = 12 \(\Omega\)
Now R12 and 6 \(\Omega\) are connected in parallel, so the net resistance is given by
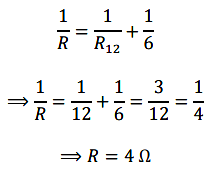
12. Several electric bulbs designed to be used on a 220 V electric supply line, are rated 10 W. How many lamps can be connected in parallel with each other across the two wires of 220 V line if the maximum allowable current is 5 A?
Answer:
For one bulb:
Power P = 10 W and Potential difference V = 220 V
Using the relation for R, we have
R = \(\frac{V^2}P=\frac{220^2}{10}\) = 4840 \(\Omega\)
Let the total number of bulbs be x.
Given that:
Current I = 5 A and Potential Difference V = 220 V
According to Ohm’s law, V = IR
R = V/I = 220/5 = 44 \(\Omega\)
Now, for x number of bulbs of resistance 176\(\Omega\), the equivalent resistance of the resistors connected in parallel is 44\(\Omega\)
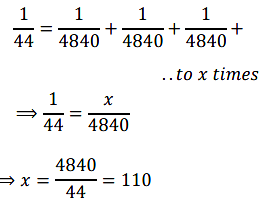
Therefore, 110 bulbs of 4840 \(\Omega\) are required to draw the given amount of current.
13. A hot plate of an electric oven connected to a 220 V line has two resistance coils A and B, each of 24 Ω resistance, which may be used separately, in series, or in parallel. What are the currents in the three cases?
Answer:
Given that:
Potential difference V = 220 V and resistance of each coil R = 24\(\Omega\)
When the coil is used separately, the current in the coil is given by
I = V/R = 220/24 = 55/6 = 9.16 A
When the two coils are connected in series, the net resistance is given by
R = R1 + R2 = 24\(\Omega\) + 24\(\Omega\) = 48\(\Omega\)
Now, the current in the coil is given by
I = V/R = 220/48 = 55/12 = 4.58 A
When the two coils are connected in parallel, the net resistance is given by
1/R = 1/24 + 1/24 = 2/24 = 1/12
Now, the current in the coil is given by
I = V/R = 220/12 = 55/3 = 18.33 A
14. Compare the power used in the 2\(\Omega\) resistor in each of the following circuits:
(i) a 6 V battery in series with 1\(\Omega\) and 2\(\Omega\) resistors, and (ii) a 4 V battery in parallel with 12\(\Omega\) and 2\(\Omega\) resistors.
Answer:
Given that:
Potential difference, V = 6 V
(i). 1 \(\Omega\) and 2 \(\Omega\) resistors are connected in series. Therefore, equivalent resistance of the circuit, R = 1 + 2 = 3\(\Omega\)
According to Ohm’s law,
V = IR
⇒ I = V/R = 6/3 = 2 A
In series combination, the current in the circuit remains constant. Therefore power is given by
P = I2R = (2)2 x 2 = 8 W
(ii). 1 \(\Omega\) and 2 \(\Omega\) resistors are connected in parallel.
⇒ I = V/R = 6/3 = 2A
In parallel combination, the voltage in the circuit remains constant. Therefore power is given by
P = \(\frac{V^2}R=\frac{4^2}2\) = 8 W
Hence, in both the cases power remains same as 8W.
15. Two lamps, one rated 100 W at 220 V, and the other 60 W at 220 V, are connected in parallel to electric mains supply. What current is drawn from the line if the supply voltage is 220 V?
Answer:
For the lamp one:
Power P1 = 100 W and Potential difference V = 220 V
Therefore,
\(I_1=\frac{P_1}{V}\) = 100/220 = 0.455 A
For the lamp two:
Power P2 = 60 W and Potential difference V = 220 V
Therefore,
\(I_1=\frac{P_2}V\) = 60/220 = 0.273 A
So, the net current drawn from the supply is given by
I = I1 + I2 = 0.455 + 0.273 = 0.728 A
16. Which uses more energy, a 250 W TV set in 1 hr, or a 1200 W toaster in minutes?
Answer:
Energy consumed by an electrical appliance is given by H = Pt
For the TV set:
Power W = 250 W and time t = 1 hour = 3600 seconds
So, energy consumed H = 250 × 3600 = 900000 J
For the toaster:
Power W = 1200 W and time t = 10 minutes = 600 seconds
So, energy consumed H = 1200 × 600 = 720000 J
Hence, TV set uses more energy than toaster.