Question

NCERT Solutions Class 11 Physics Chapter 7 System of Particles and Rotational Motion is a great way of learning about the important concepts of physics. Our NCERT Solutions have an in-depth analysis of all the concepts discussed here. Our NCERT solutions are an amazing way to learn about the basic concepts of this chapter, prepare for board examinations, and also for clearing tough competitive exams like JEE Mains, NTSE, JEE Advance, and Olympiad.

In NCERT Solutions Class 11 we have prepared the solutions in such a way that it is easy to understand and learn for examination. Our experts at Sarthaks suggest learning every concept of the chapter to gain clarity on the subject. Important concepts mentioned in the chapter are:

• Motions of a rigid body and the center of mass of particles and its mathematical equations.
• Newton's second law of motion and linear momentum in a system of particles.
• Vector product and the vector product obtained from two vectors.
• Relationship between angular and linear velocity with the help of various diagrams and numerical.
• Torque – The force used for rotating an object on its axis.
• Relation between torque and angular momentum and angular acceleration.
• Angular momentum of a particle and the conservation of angular momentum.
• Linear momentum of a rigid body changes when force is applied to it.
• Equilibrium attained in a rigid body.
• Equations and theorems for the center of gravity.
• Kinetic energy of a rotating body and moment of inertia.
• Theorems of perpendicular and parallel axes.
• Dynamic, kinematic, and angular momentum derivations in rotational motion on a fixed axis.
• Rolling motions of an object and kinetic energy possessed by it.
• Radius of Gyration – the root mean square distance of its constituent particle from the axis of rotation is called the radius of gyration of a body.

Our NCERT Solutions Class 11 Physics is explained in the point-wise method with the help of diagrams, shortcuts, tips, and tricks to help students remember the subject material with complete clarity. Our solutions also provide in-text question solutions and practical based questions.

Get started now to ace your examination.

Answer 1

NCERT Solutions Class 11 Physics Chapter 7 System of particles and Rotational Motion

1. Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body? 

Solution:

Geometric centre; No 

The centre of mass (C.M.) is a point where the mass of a body is supposed to be concentrated. For the given geometric shapes having a uniform mass density, the C.M. lies at their respective geometric centres.

The centre of mass of a body need not necessarily lie within it. For example, the C.M. of bodies such as a ring, a hollow sphere, etc., lies outside the body.

2. In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus. 

Solution:

The given situation can be shown as: 

Distance between H and Cl atoms = 1.27Å

Mass of H atom = m 

Mass of Cl atom = 35.5m 

Let the centre of mass of the system lie at a distance x from the Cl atom. 

Distance of the centre of mass from the H atom = (1.27 – x) 

Let us assume that the centre of mass of the given molecule lies at the origin. Therefore, we can have:

Here, the negative sign indicates that the centre of mass lies at the left of the molecule. Hence, the centre of mass of the HCl molecule lies 0.037Å from the Cl atom. 

3. A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system? 

Solution:

No change

The child is running arbitrarily on a trolley moving with velocity v. However, the running of the child will produce no effect on the velocity of the centre of mass of the trolley. This is because the force due to the boy’s motion is purely internal. Internal forces produce no effect on the motion of the bodies on which they act. Since no external force is involved in the boy–trolley system, the boy’s motion will produce no change in the velocity of the centre of mass of the trolley.

4. Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of a x b

Solution:

Consider two vectors \(\overrightarrow {OK} = |\overrightarrow a| \, and\, \overrightarrow {OM} = |\overrightarrow b|\), inclined at an angle θ, as shown in the following figure.

In ΔOMN, we can write the relation:

= 2 × Area of ΔOMK

∴ Area of ΔOMK = \(\frac 12|\overrightarrow a \times \overrightarrow b|\)

5. Show that a. (b × c) is equal in magnitude to the volume of the parallelepiped formed on the three vectors, a, b and c.

Solution:

A parallelepiped with origin O and sides a, b, and c is shown in the following figure.

Volume of the given parallelepiped = abc

Let be \(\hat n\) a unit vector perpendicular to both b and c. Hence, \(\hat n\) and a have the same direction.

= abc cosθ \(\hat n\)

= abc cos 0° 

= abc 

= Volume of the parallelepiped

Answer 2

 6. Find the components along the x, y, z axes of the angular momentum l of a particle, whose position vector is r with components x, y, z and momentum is p with components p_x, p_y and p_z. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.

Solution:

l_x = yp_z – zp_y l_y 

= zp_x – xp_z l_z 

= xp_y –yp_x 

Linear momentum of the particle, \(\overrightarrow p = p_x\hat i + p_y \hat j + p_z \hat k\)

Position vector of the particle, \(\overrightarrow r = x\hat i + y \hat j + z \hat k\)

Angular momentum, \(\overrightarrow l = \overrightarrow r \times \overrightarrow p\)

= (\(x\hat i + y \hat j + z \hat k\)) x (\(p_x\hat i + p_y \hat j + p_z \hat k\) )

= \(\begin {vmatrix}\hat i & \hat j & \hat k \\x&y&z\\p_x&p_y&p_z\end {vmatrix}\)

\(l_x \hat i + l_y \hat j + l_z \hat k = \hat i ( yp_z - zp_y) - \hat j (xp_z - zp_z - zp_x) + \hat k (xp_y - zp_x)\)

Comparing the coefficients of we \(\hat i, \hat j,\) and \(\hat k\) get:

The particle moves in the x-y plane. Hence, the z-component of the position vector and linear momentum vector becomes zero, i.e., z = p_z = 0 

Thus, equation (i) reduces to:

Therefore, when the particle is confined to move in the x-y plane, the direction of angular momentum is along the z-direction.

7. Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two particle system is the same whatever be the point about which the angular momentum is taken. 

Solution:

Let at a certain instant two particles be at points P and Q, as shown in the following figure.

Angular momentum of the system about point P:

\(\overrightarrow L_P\) = mv x 0 + mv x d = mvd ........(i)

Angular momentum of the system about point Q:

 \(\overrightarrow L_Q\) = mv x 0 + mv x d = mvd ........(ii)

Consider a point R, which is at a distance y from point Q, i.e., 

QR = y 

∴ PR = d – y 

Angular momentum of the system about point R:

 \(\overrightarrow L_R\) = mv x (d-y) + mv x y 

= mvd - mvy + mvy

= mvd   ........(iii)

Comparing equations (i), (ii), and (iii), we get:

\(\overrightarrow L_P\)= \(\overrightarrow L_Q\) = \(\overrightarrow L_R\).....(iv)

We infer from equation (iv) that the angular momentum of a system does not depend on the point about which it is taken.

8. A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Figure. The angles made by the strings with the vertical are 36.9° and 53.1° respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.

Solution:

The free body diagram of the bar is shown in the following figure.

Length of the bar, l = 2 m 

T₁ and T₂ are the tensions produced in the left and right strings respectively. 

At translational equilibrium, we have:

For rotational equilibrium, on taking the torque about the centre of gravity, we have:

= 0.72 m

Hence, the C.G. (centre of gravity) of the given bar lies 0.72 m from its left end.

9. A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.

Solution:

Mass of the car, m = 1800 kg 

Distance between the front and back axles, d = 1.8 m 

Distance between the C.G. (centre of gravity) and the back axle = 1.05 m 

The various forces acting on the car are shown in the following figure.

R_f and R_b are the forces exerted by the level ground on the front and back wheels respectively.

At translational equilibrium:

R_f + R_b = mg

= 1800 × 9.8 

= 17640 N … (i) 

For rotational equilibrium, on taking the torque about the C.G., we have:

Solving equations (i) and (ii), we get:

∴ R_b = 17640 – 7350 = 10290 N

Therefore, the force exerted on each front wheel = \(\frac {7350}{2}\) = 3675 , and 

The force exerted on each back wheel = \(\frac {10290}{2}\) = 5145 N

Answer 3

10. Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR^2/5, where M is the mass of the sphere and R is the radius of the sphere.

Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR^2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge.

Solution:

\(\frac 75 MR^2\)

The moment of inertia (M.I.) of a sphere about its diameter = \(\frac 25 MR^2\)

M.I = \(\frac 25 MR^2\) 

According to the theorem of parallel axes, the moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.

The M.I. about a tangent of the sphere = \(\frac 25 MR^2\) + MR² =  \(\frac 75 MR^2\) 

(b) \(\frac 32 MR^2\) 

The moment of inertia of a disc about its diameter = \(\frac 14 MR^2\) 

According to the theorem of perpendicular axis, the moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with perpendicular axis and lying in the plane of the body.

The M.I. of the disc about its centre = \(\frac 14 MR^2\) + \(\frac 14 MR^2\) = \(\frac 12 MR^2\)

The situation is shown in the given figure.

Applying the theorem of parallel axes: 

The moment of inertia about an axis normal to the disc and passing through a point on

its edge = \(\frac 12 MR^2\) + MR² = \(\frac 32 MR^2\)

11. Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?

Solution :

Let m and r be the respective masses of the hollow cylinder and the solid sphere.

The moment of inertia of the hollow cylinder about its standard axis, l₁ = mr²

The moment of inertia of the solid sphere about an axis passing through its centre,

l₁₁ = \(\frac 25 mr^2\)

We have the relation:

T = la

Where, α = Angular 

acceleration T = Torque

I = Moment of inertia 

For the hollow cylinder, T₁ = l₁a₁

For the solid sphere, T₁₁ = l₁₁a₁₁

As an equal torque is applied to both the bodies, T₁ = T₂

Now, using the relation:

ω = ω₀ + at

Where,

ω₀ = Initial angular velocity 

t = Time of rotation ω = 

Final angular velocity For equal ω₀ and t, we have: 

ω α … (ii) 

From equations (i) and (ii), we can write: 

ω_II > ω_I 

Hence, the angular velocity of the solid sphere will be greater than that of the hollow cylinder. 

12. A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s^–1 . The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis? 

Solution: 

Mass of the cylinder, m = 20 kg 

Angular speed, ω = 100 rad s^–1 

Radius of the cylinder, r = 0.25 m 

The moment of inertia of the solid cylinder:

l = \(\frac {mr^2}{2}\) 

= \(\frac 12\) x 20 x (0.25)²

= 0.625 kg m²

∴ Kinetic energy = \(\frac 12\) lω²

= \(\frac 12\) x 6.25 x (100)² 

= 3125 J

∴ Angular momentum, L = Iω

= 6.25 × 100 

= 62.5 Js

13. A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value? Assume that the turntable rotates without friction. 

Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy? 

Solution:

100 rev/min 

Initial angular velocity, ω₁= 40 rev/min 

Final angular velocity = ω₂ 

The moment of inertia of the boy with stretched hands = I₁

The moment of inertia of the boy with folded hands = I₂

The two moments of inertia are related as:

I₂ = \(\frac 25 l_1\) 

Since no external force acts on the boy, the angular momentum L is a constant. 

Hence, for the two situations, we can write:

I

= 100 rev/min

(b) Final K.E. = 2.5 Initial K.E.

Final kinetic rotation, E_F=   \(\frac 12\) l₂ω²

Initial kinetic rotation, E_I =   \(\frac 12\) l₁\(ω^2_1\)

∴ E_F = 2.5 E₁

The increase in the rotational kinetic energy is attributed to the internal energy of the boy.

14. A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping. 

Solution:

Mass of the hollow cylinder, m = 3 kg 

Radius of the hollow cylinder, r = 40 cm = 0.4 m 

Applied force, F = 30 N

The moment of inertia of the hollow cylinder about its geometric axis: 

I = mr² 

= 3 × (0.4)² = 0.48 kg m² 

Torque, = T = F x r

30 × 0.4 = 12 Nm 

For angular acceleration a, torque is also given by the relation:

T = la

a = \(\frac Tl = \frac {12}{0.48}\) 

= 25 rad s^-2

Linear acceleration = rα = 0.4 × 25 = 10 m s^–2

Answer 4

15. To maintain a rotor at a uniform angular speed of 200 rad s^–1 , an engine needs to transmit a torque of 180 Nm. What is the power required by the engine? 

(Note: uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter frictional torque). Assume that the engine is 100 % efficient. 

Solution:

Angular speed of the rotor, ω = 200 rad/s 

Torque required, τ = 180 Nm

The power of the rotor (P) is related to torque and angular speed by the relation: 

P = τω 

= 180 × 200 = 36 × 10³ 

= 36 kW 

Hence, the power required by the engine is 36 kW.

16. From a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body. 

Solution:

R/6; from the original centre of the body and opposite to the centre of the cut portion. 

Mass per unit area of the original disc = σ 

Radius of the original disc = R 

Mass of the original disc, M = πR²σ 

The disc with the cut portion is shown in the following figure:

Radius of the smaller disc = \(\frac R2\)

Mass of the smaller disc, M’ = \(\pi (\frac R2)^2 σ = \frac 14 \pi R^2 σ = \frac M4\) 

Let O and O′ be the respective centres of the original disc and the disc cut off from the original. As per the definition of the centre of mass, the centre of mass of the original disc is supposed to be concentrated at O, while that of the smaller disc is supposed to be concentrated at O′. 

It is given that:

OO' = \(\frac R2\) 

After the smaller disc has been cut from the original, the remaining portion is considered to be a system of two masses. The two masses are: 

M (concentrated at O), and

-M'(= \(\frac M4\) ) concentrated at O′

(The negative sign indicates that this portion has been removed from the original disc.) 

Let x be the distance through which the centre of mass of the remaining portion shifts from point O. 

The relation between the centres of masses of two masses is given as:

x = \(\frac {m_1r_1 + m_2 r_2}{m_1 + m_2}\) 

For the given system, we can write:

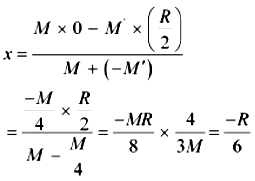
(The negative sign indicates that the centre of mass gets shifted toward the left of point O.)

17. A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick? 

Solution:

Let W and W′ be the respective weights of the metre stick and the coin.

The mass of the metre stick is concentrated at its mid-point, i.e., at the 50 cm mark. 

Mass of the meter stick = m’ 

Mass of each coin, m = 5 g

When the coins are placed 12 cm away from the end P, the centre of mass gets shifted by 5 cm from point R toward the end P. The centre of mass is located at a distance of 45 cm from point P.

The net torque will be conserved for rotational equilibrium about point R.

10 x g (45 - 12) -m'g (50 -45) = 0

∴ m'= \(\frac {10\times33}{5}\) = 66 g

Hence, the mass of the metre stick is 66 g.

18. A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. 

(a) Will it reach the bottom with the same speed in each case? 

(b) Will it take longer to roll down one plane than the other? 

(c) If so, which one and why? 

Solution:

(a) Yes (b) Yes (c) On the smaller inclination 

(a)Mass of the sphere = m 

Height of the plane = h 

Velocity of the sphere at the bottom of the plane = v 

At the top of the plane, the total energy of the sphere = Potential energy = mgh 

At the bottom of the plane, the sphere has both translational and rotational kinetic energies. 

Hence, total energy = \(\frac 12 mv^2 + \frac 12 l\)ω²

Using the law of conservation of energy, we can write:

\(\frac 12 mv^2 + \frac 12 l\) ω²= mgh ....(i)

For a solid sphere, the moment of inertia about its centre, I = \(\frac 25 mr^2 \)

Hence, equation (i) becomes: 

\(\frac 12 mv^2 + \frac 12 \) (\(\frac 25 mr^2 \))ω² = mgh

 \(\frac 12 v^2 + \frac 15 v^2\) = gh

v² (\(\frac {7}{10}\)) = gh

v = \(\sqrt{\frac {7}{10}}gh\) 

Hence, the velocity of the sphere at the bottom depends only on height (h) and acceleration due to gravity (g). Both these values are constants. Therefore, the velocity at the bottom remains the same from whichever inclined plane the sphere is rolled. 

(b), (c) Consider two inclined planes with inclinations θ₁ and θ₂, related as: θ₁ < θ₂

The acceleration produced in the sphere when it rolls down the plane inclined at θ₁ is: g sin θ₁ 

The various forces acting on the sphere are shown in the following figure.

R₁ is the normal reaction to the sphere. 

Similarly, the acceleration produced in the sphere when it rolls down the plane inclined at θ₂ is: g sin θ₂ 

The various forces acting on the sphere are shown in the following figure.

R₂ is the normal reaction to the sphere. 

θ₂ > θ₁; sin θ₂ > sin θ₁ ... (i) 

∴ a₂ > a₁ … (ii) 

Initial velocity, u = 0 

Final velocity, v = Constant 

Using the first equation of motion, we can obtain the time of roll as: 

v = u + at

∴ t ∝ \(\frac 1a\)

For inclination θ₁ : t₁ ∝ \(\frac 1{a_1}\) 

 For inclination θ₂ : t₂ ∝ \(\frac 1{a_2}\) 

From equations (ii) and (iii), we get:

t₂ < t₁

Hence, the sphere will take a longer time to reach the bottom of the inclined plane having the smaller inclination.

Answer 5

19. A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm/s. How much work has to be done to stop it?

Solution:

Radius of the hoop, r = 2 m 

Mass of the hoop, m = 100 kg 

Velocity of the hoop, v = 20 cm/s = 0.2 m/s 

Total energy of the hoop = Translational KE + Rotational KE

E_T = \(\frac 12mv^2 + \frac 12lω^2\) 

Moment of inertia of the hoop about its centre, I = mr²

E_T = \(\frac 12mv^2 + \frac 12(mr^2)ω^2\)

But we have the relation, v = rω

∴  E_T = \(\frac 12mv^2 + \frac 12(mr^2)ω^2\)

=  \(\frac 12mv^2 + \frac 12mv^2 = mv^2\) 

The work required to be done for stopping the hoop is equal to the total energy of the hoop.

∴ Required work to be done, W = mv² = 100 × (0.2)² = 4 J

20. The oxygen molecule has a mass of 5.30 × 10^–26 kg and a moment of inertia of 1.94×10^–46 kg m² about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule. 

Solution:

Mass of an oxygen molecule, m = 5.30 × 10^–26 kg 

Moment of inertia, I = 1.94 × 10^–46 kg m² 

Velocity of the oxygen molecule, v = 500 m/s 

The separation between the two atoms of the oxygen molecule = 2r

Mass of each oxygen atom = \(\frac m2\)

Hence, moment of inertia I, is calculated as:

It is given that:

21. A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane the centre of mass of the cylinder has a speed of 5 m/s. 

How far will the cylinder go up the plane? 

How long will it take to return to the bottom?

Solution:

A solid cylinder rolling up an inclination is shown in the following figure.

Initial velocity of the solid cylinder, v = 5 m/s 

Angle of inclination, θ = 30° 

Height reached by the cylinder = h Energy of the cylinder at point

A:

Energy of the cylinder at point B = mgh

Using the law of conservation of energy, we can write:

\(\frac 12lω^2 = \frac 12mv^2\) = mgh

Moment of inertia of the solid cylinder, l = \(\frac 12mr^2\)

But we have the relation, v = rω

∴ \(\frac 14v^2 + \frac 12v^2 = gh\)

\(\frac 34v^2 = gh\)

∴ h = \(\frac 34\frac {v^2}{g}\)

= \(\frac 34\times \frac {5 \times 5}{9.8}\) = 1.91 m

In ΔABC:

Hence, the cylinder will travel 3.82 m up the inclined plane. 

For radius of gyration K, the velocity of the cylinder at the instance when it rolls back to the bottom is given by the relation:

The time taken to return to the bottom is:

Therefore, the total time taken by the cylinder to return to the bottom is (2 × 0.764) 1.53 s.

Answer 6

22. As shown in Figure, the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F, 1.2 m from B along the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g = 9.8 m/s²) (Hint: Consider the equilibrium of each side of the ladder separately.)

Solution:

The given situation can be shown as:

NB = Force exerted on the ladder by the floor point B NC = Force exerted on the ladder by the floor point C T = Tension in the rope BA = CA = 1.6 m DE = 0. 5 m BF = 1.2 m Mass of the weight, m = 40 kg Draw a perpendicular from A on the floor BC. This intersects DE at mid-point H. ΔABI and ΔAIC are similar BI = IC Hence, I is the mid-point of BC. DE || BC BC = 2 × DE = 1 m AF = BA – BF = 0.4 m … (i) D is the mid-point of AB. Hence, we can write:

AD = \(\frac 12 \) x BA = 0.8 m .....(ii)

Using equations (i) and (ii), we get: 

FE = 0.4 m

Hence, F is the mid-point of AD. 

FG||DH and F is the mid-point of AD. Hence, G will also be the mid-point of AH. 

ΔAFG and ΔADH are similar

For translational equilibrium of the ladder, the upward force should be equal to the downward force. Nc + NB = mg = 392 … (iii) For rotational equilibrium of the ladder, the net moment about A is:

Adding equations (iii) and (iv), we get:

N_C = 245 N

N_B = 147 N

For rotational equilibrium of the side AB, consider the moment about A.

23. A man stands on a rotating platform, with his arms stretched horizontally holding a 5 kg weight in each hand. The angular speed of the platform is 30 revolutions per minute. The man then brings his arms close to his body with the distance of each weight from the axis changing from 90cm to 20cm. The moment of inertia of the man together with the platform may be taken to be constant and equal to 7.6 kg m². 

What is his new angular speed? (Neglect friction.) 

Is kinetic energy conserved in the process? If not, from where does the change come about? 

Solution:

58.88 rev/min (b) No 

(a) Moment of inertia of the man-platform system = 7.6 kg m² 

Moment of inertia when the man stretches his hands to a distance of 90 cm: 

2 × m r² 

= 2 × 5 × (0.9)²

= 8.1 kg m² 

Initial moment of inertia of the system, L_i = 7.6 + 8.1 = 17.7 kg m²

Angular speed, ω_i = 300 rev/min

Angular momentum, L_i = l_iω_i = 15.7 x 30 ....(i)

Moment of inertia when the man folds his hands to a distance of 20 cm:

2 x m r²

= 2 x 5 (0.2)² = 0.4 kg m²

Final moment of inertia, l_f = 7.6 + 0.4 = 8 kg m²

Final angular speed = ω_f

Final angular momentum, L_f = l_fω_f = 0.79 ω_f ....(ii)

From the conservation of angular momentum, we have:

l_iω_i = l_iω_f 

∴ ω_f = \(\frac {15.7 \times 30}{8} \) = 58.88 rev/min

(b)Kinetic energy is not conserved in the given process. In fact, with the decrease in the moment of inertia, kinetic energy increases. The additional kinetic energy comes from the work done by the man to fold his hands toward himself.

24. A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.

(Hint: The moment of inertia of the door about the vertical axis at one end is ML^2/3.) 

Solution:

Mass of the bullet, m = 10 g = 10 × 10^–3 kg 

Velocity of the bullet, v = 500 m/s 

Thickness of the door, L = 1 m 

Radius of the door, r = \(\frac 12\)m

Mass of the door, M = 12 kg 

Angular momentum imparted by the bullet on the door: 

α = mvr

= (10 x 10^-3) x (500) x \(\frac 12\) = 2.5 kg m²s^-1 ....(i)

Moment of inertia of the door:

l = \(\frac 13\)ML²

= \(\frac 13\)x 12 x (1)² = 4kg m²

But a = lω

∴ ω = \(\frac al\)

= \(\frac {2.5}{4}\) = 0.625 rad s^-1

Answer 7

 25. Two discs of moments of inertia I₁ and I₂ about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ω₁ and ω₂ are brought into contact face to face with their axes of rotation coincident. 

(a) What is the angular speed of the two-disc system? 

(b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take ω₁ ≠ ω₂.

Solution:

Moment of inertia of disc I = l₁

Angular speed of disc I = ω₁

Angular speed of disc II = l₂

Angular momentum of disc II = ω₁

Angular momentum of disc I, L₁ =  l₁ω₁

Angular momentum of disc II, L₂ =  l₂ω₂

Total initial angular momentum, L_i = l₁ω₁ +  l₂ω₂

When the two discs are joined together, their moments of inertia get added up.

Moment of inertia of the system of two discs, l = l₁ + l₂

Let ω be the angular speed of the system.

Total final angular momentum, L_f = (l₁ + l₂)ω

Using the law of conservation of angular momentum, we have:

L_i = L_f

(b)Kinetic energy of disc I, E₁ = \(\frac 12\) l₁\(ω^2_1\)

 (b)Kinetic energy of disc II, E₂ = \(\frac 12\) l₂\(ω^2_2\) 

Total initial kinetic energy, Ei = \(\frac 12\) ( l₁\(ω^2_1\) +  l₂\(ω^2_2\) )

When the discs are joined, their moments of inertia get added up. 

Moment of inertia of the system, l = l₁ + l₂

Angular speed of the system = ω 

Final kinetic energy E_f:

Al the quantities on RHS are positive

∴ E_i - E_f > 0

E_i > E_f

The loss of KE can be attributed to the frictional force that comes into play when the two discs come in contact with each other.

26. Prove the theorem of perpendicular axes.

(Hint: Square of the distance of a point (x, y) in the x–y plane from an axis through the origin perpendicular to the plane is x² + y²).

Prove the theorem of parallel axes. 

(Hint: If the centre of mass is chosen to be the origin \(\sum m_1r_1=0).\) 

Solution:

(a)The theorem of perpendicular axes states that the moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with perpendicular axis and lying in the plane of the body. 

A physical body with centre O and a point mass m, in the x–y plane at (x, y) is shown in the following figure.

Moment of inertia about x-axis, I_x = mx² 

Moment of inertia about y-axis, I_y = my² 

Moment of inertia about z-axis, I_z = \(m(\sqrt {x^2 + y^2})^2\)

I_x + I_y = mx² + my²

= m(x² + y²)

= \(m(\sqrt {x^2 + y^2})^2\)

I_x + I_y = I_z

(b)The theorem of parallel axes states that the moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.

Suppose a rigid body is made up of n particles, having masses m₁, m₂, m₃, … , m_n, at perpendicular distances r₁, r₂, r₃, … , r_n respectively from the centre of mass O of the rigid body. 

The moment of inertia about axis RS passing through the point O:

I_RS = \(\sum\limits_{i=1}^n m_1r_1^2\) 

The perpendicular distance of mass mi, from the axis QP = a + r_i 

Hence, the moment of inertia about axis QP:

Now, at the centre of mass, the moment of inertia of all the particles about the axis passing through the centre of mass is zero, that is,

Hence, the theorem is proved

27. Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by

v² = \(\frac {2gh}{(1+k^2 | R^2)}\)

Using dynamical consideration (i.e. by consideration of forces and torques). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.

Solution:

A body rolling on an inclined plane of height h, is shown in the following figure:

m = Mass of the body 

R = Radius of the body 

K = Radius of gyration of the body 

v = Translational velocity of the 

body h =Height of the inclined 

plane g = Acceleration due to gravity 

Total energy at the top of the plane, E₁= mgh

Total energy at the bottom of the plane, E_b = KE_rot + KE_trans

= \(\frac 12 Iω^2 + \frac 12mv^2\)

But I = mk² and ω = \(\frac VR\) 

From the law of conservation of energy, we have:

E_T = E_b

mgh = \( \frac 12mv^2\) (1 + \(\frac {k^2}{R^2}\) )

∴ v = \(\frac {2gh}{(1 + k^2| R^2)}\)

Hence, the given result is proved.

Answer 8

28. A disc rotating about its axis with angular speed ωois placed lightly (without any translational push) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A, B and C on the disc shown in Figure? Will the disc roll in the direction indicated?

Solution:

v_A = Rω_o; v_B = Rω_o; v_c = (\(\frac R2\))ω_o; The disc will not roll Angular speed of the disc = ω_o

Radius of the disc = R 

Using the relation for linear velocity, v = ω_oR

For point A: 

v_A = Rω_o; in the direction tangential to the right 

For point B: 

v_B = Rω_o; in the direction tangential to the left 

For point C:

 v_c = (\(\frac R2\))ω_o; in the direction same as that of v_A

The directions of motion of points A, B, and C on the disc are shown in the following figure

Since the disc is placed on a frictionless table, it will not roll. This is because the presence of friction is essential for the rolling of a body.

29. A solid disc and a ring, both of radius 10 cm are placed on a horizontal table simultaneously, with initial angular speed equal to 10 π rad s^-1. Which of the two will start to roll earlier? The co-efficient of kinetic friction is μ_k = 0.2.

Solution: 

Disc Radii of the ring and the disc, r = 10 cm = 0.1 m 

Initial angular speed, ω₀ =10 π rad s^–1 

Coefficient of kinetic friction, μk = 0.2 

Initial velocity of both the objects, u = 0

Motion of the two objects is caused by frictional force. As per Newton’s second law of motion, we have frictional force, f = ma μkmg= ma Where, a = Acceleration produced in the objects m = Mass ∴ a = μ_kg … (i) 

As per the first equation of motion, the final velocity of the objects can be obtained as: 

v = u + at 

= 0 + μ_kgt 

= μ_kgt … (ii)

The torque applied by the frictional force will act in perpendicularly outward direction and cause reduction in the initial angular speed.

Torque, τ= –Iα 

α = Angular acceleration μxmgr = –Iα

∴ a = \(\frac {-μ_kmgr}{1}\) ...(iii)

Using the first equation of rotational motion to obtain the final angular speed:

ω = ω₀ + at

= ω₀ + \(\frac {-μ_kmgr}{1}\)t ...(iv)

Rolling starts when linear velocity, v = rω

∴ v = r (ω₀ - \(\frac {μ_kmgrt}{1}\)) .....(v)

Equating equations (ii) and (v), we get:

μ_kgt =  r ( ω₀ + \(\frac {μ_kmgrt}{1}\))

= rω₀  - \(\frac {μ_kmgr^2t}{1}\) ......(vi)

For the ring: I = mr²

Since t_d > t_r, the disc will start rolling before the ring.

30. A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of static friction µ_s = 0.25. How much is the force of friction acting on the cylinder? What is the work done against friction during rolling? If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly? 

Solution:

Mass of the cylinder, m = 10 kg 

Radius of the cylinder, r = 15 cm = 0.15 m 

Co-efficient of kinetic friction, µ_k = 0.25 

Angle of inclination, θ = 30° 

Moment of inertia of a solid cylinder about its geometric axis, I = \(\frac 12mr^2\)

The various forces acting on the cylinder are shown in the following figure:

The acceleration of the cylinder is given as:

Using Newton’s second law of motion, we can write net force as: 

f_net = ma

mg sin 30° - f = ma

f = mg sin 30° - ma

= 10 x 9.8 x 0.5 - 10 x 3.27

= 49 - 32.7 = 16.3 N

During rolling, the instantaneous point of contact with the plane comes to rest. Hence, the work done against frictional force is zero. 

For rolling without skid, we have the relation:

μ = \(\frac 13\) tan θ

tan θ = 3 μ = 3 x 0.25

∴ θ = tan-1 (0.75) = 36.87°

 31. Read each statement below carefully, and state, with reasons, if it is true or false; 

a) During rolling, the force of friction acts in the same direction as the direction of motion of the CM of the body. 

b) The instantaneous speed of the point of contact during rolling is zero. 

c) The instantaneous acceleration of the point of contact during rolling is zero. 

d) For perfect rolling motion, work done against friction is zero. 

e) A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling) motion. 

Solution:

a) False 

Frictional force acts opposite to the direction of motion of the centre of mass of a body. In the case of rolling, the direction of motion of the centre of mass is backward. Hence, frictional force acts in the forward direction. 

b) True 

Rolling can be considered as the rotation of a body about an axis passing through the point of contact of the body with the ground. Hence, its instantaneous speed is zero. 

c) False 

When a body is rolling, its instantaneous acceleration is not equal to zero. It has some value. 

d) True 

When perfect rolling begins, the frictional force acting at the lowermost point becomes zero. Hence, the work done against friction is also zero. 

e) True

The rolling of a body occurs when a frictional force acts between the body and the surface. This frictional force provides the torque necessary for rolling. In the absence of a frictional force, the body slips from the inclined plane under the effect of its own weight.

Answer 9

 32. Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass: 

Show p_i = p’_i + m_iV 

Where p_i is the momentum of the i^th particle (of mass mi) and p′_i = m_i v′_i. Note v′_i is the velocity of the i^th particle relative to the centre of mass.

Also, prove using the definition of the centre of mass \(\sum_ \limits i p'_i = 0\)

Show K = K′ + \(\frac 12\)MV² 

Where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV^2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system).

Show L = L'+ R x MN

Where'= \(\sum_ \limits i r'_i \times p'_i\) is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember r’_i = r_i – R; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.

Show \(\frac {dL'}{dt} = \sum \limits_i r'_i \times \frac {d}{dt} (p'_i)\) 

Further, show that

\(\frac {dL'}{dt} = T'_{ext}\)

where T'_ext is the sum of all external torques acting on the system about the centre of mass.

(Hint: Use the definition of centre of mass and Newton’s Third Law. Assume the internal forces between any two particles act along the line joining the particles.)

Solution:

(a)Take a system of i moving particles. 

Mass of the i^th particle = m_i 

Velocity of the i^th particle = v_i 

Hence, momentum of the i^th particle, p_i = m_i v_i 

Velocity of the centre of mass = V 

The velocity of the i^th particle with respect to the centre of mass of the system is given as: 

v’_i = v_i – V … (1) 

Multiplying m_i throughout equation (1), we get: 

m_i v’_i = m_i v_i – m_i V 

p’_i = p_i – m_i V 

Where,

p_i’ = m_iv_i’ = Momentum of the i^th particle with respect to the centre of mass of the system 

∴ p_i = p’_i +m_i V 

We have the relation: p’_i = m_iv_i’ 

Taking the summation of momentum of all the particles with respect to the centre of mass of the system, we get:

Where,

rí = Position vector of ith particle with respect to the centre of mass

ví = \(\frac {dr'_i}{dt}\) 

As per the definition of the centre of mass, we have:

\(\sum \limits_i m_ir'_i = 0\)

∴ \(\sum \limits_i m_i\frac {dr'_i}{dt} = 0\) 

\(\sum \limits_i p'_i = 0\) 

We have the relation for velocity of the i^th particle as: 

v_i = v’_i + V

Taking the dot product of equation (2) with itself, we get:

Here, for the centre of mass of the system of particles, \(\sum \limits_i v_i.v'_i = -\sum \limits_i vi_i.v_i\)

K = K'+ \(\frac 12MV^2\) 

Where,

K = \(\frac 12M \sum \limits_iv^2_i\) = Total kinetic energy of the system of particles

K = \(\frac 12M \sum \limits_iv'^2_i\) = Total kinetic energy of the system of particles with respect to the centre of mass

\(\frac 12MV^2\) = Kinetic energy of the translation of the system as a whole

Position vector of the i^th particle with respect to origin = r_i

Position vector of the i^th particle with respect to the centre of mass = r’_i 

Position vector of the centre of mass with respect to the origin = R

It is given that: r’_i = r_i 

– R r_i = r’_i + R 

We have from part (a), p_i 

= p’_i +m_i V 

Taking the cross product of this relation by r_i, we get:

Where,

R x \(\sum \limits_i p'_i = 0 \) and 

We have the relation:

Where, r'_i is the position vector wit respect to the centre of mass of the system of particles.

We have the relation:

Where, \(\frac {d}{dt} (v'_i)\) is the rate of change of velocity of the i^th particle with respect of the centre of mass of the system

Therefore, according to Newton's third law of motion, we can write:

m_i \(\frac {d}{dt} (v'_i)\) = External force acting on the i^th particle = \(\sum \limits _i(T'_i)_{ext}\)

i.e. \(\sum \limits_ir'_i \) x m_i \(\frac {d}{dt} (v'_i)\) = T'_ext = External torque acting on the system as a whole 

∴ \(\frac {dL'}{dt} = T'_{ext}\)