The given system of equations:
2x-3y+6=0 and 2x+3y-18=0
Now,2x-3y+6=0
y= (2x+6)/3
When x=0, then y=2
When x=-3, then y=0
Thus, we have the following table:
We have
2x+3y-18=0
X= 18−3y/2
When y=2, then x=6
When y=6, then x=0
Thus, we have the following table:
Graph of the given system of equations:
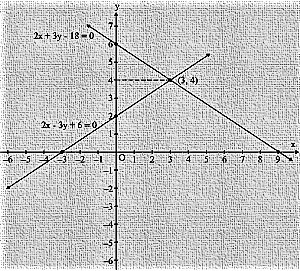
Clearly, the two lines intersect at A(3,4) .Hence x=3 and y=4 is the solution of the given system of equations.
From the graph, we have
AD=x-coordinate point A(3,4) =3
BC=6-2 = 4
Area of the shaded region = 1/2×base×altitude
= 1/2×4×3
= 6 sq. units