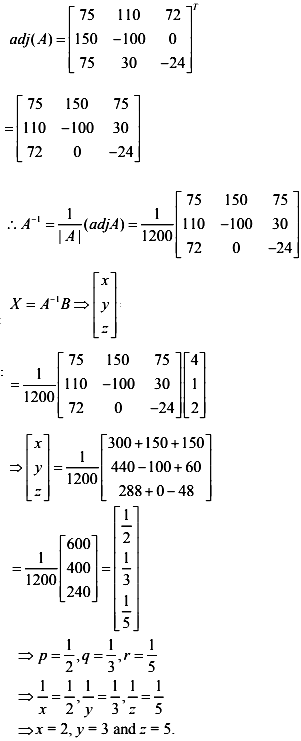Let 1/x = p, 1/y = q and 1/z = r, then the given equations become
2p + 3q + 10r = 4, 4p − 6q + 5r = 1, 6p + 9q − 20r = 2
This system can be written as AX = B, where
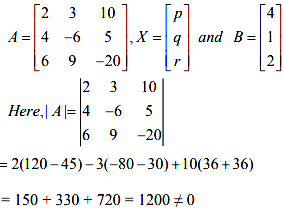
Thus, A is non-singular. Therefore, its inverse exists. Therefore, the above system is consistent and has a unique solution given by X = A −1B
Cofactors of A are
A11 = 120 − 45 = 75,
A12 = − ( − 80 − 30) = 110,
A13 = (36 + 36) = 72,
A21 = − ( − 60 − 90) = 150,
A22 = ( − 40 − 60) = − 100,
A23 = − (18 − 18) = 0,
A31 = 15 + 60 = 75,
A32 = − (10 − 40) = 30,
A33 = − 12 − 12 = − 24