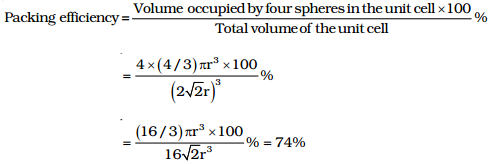Packing Fraction of Face-Centred Cubic Lattice

Let ‘r’ be the radius of sphere and ‘a’ be the edge length of the cube
As there are 4 sphere in fcc unit cell
∴ Volume of four spheres = 4 (4/3 πr3)
In fcc, the corner spheres are in touch with the face centred sphere. Therefore, face diagonal AD is equal to four times the radius of sphere
AC= 4r
But from the right angled triangle ACD
AC = √AD2 + DC2 = √a2 + a2= √2a
4r = √2a
or a = 4/√2 r
∴ volume of cube = (2/√2 r)3