The locus of all the particles of the medium, which at any instant are vibrating in the same phase, is called the wavefront.
Verification of Iaws of reflection on the basis of wave theory of light :
Let XY be a reflecting surface and PA ba a plane wavefront just incident rays.The normals LA and MP to the wavefront represent incident rays.Let AN is normal the reflecting surface at A,then ∠NAL = i is angle of incidence. The wavefront reaches at point A on the reflecting surface first of all and then in between A and P' later in time but in this order and in the last reaches at point p'.when the distubance from point p has reaches point P', the secondary wavelet from point A on the reflecting surface grows into a sphere of radius AA', such that AA' =PP'.

Draw a sphere of radius AA' = PP'. From P', draw P'A' tangent plane to the sphere. The P'A' tangent plane to the sphere.Then P'A' represents reflected wave front and normal A'L' and P'M' to the reflected wavefront P'A' represent reflected rays. Draw P'N' normal to reflecting surface at point P'. Then ∠M'P'N' = r is angle of reflection.
Consider any point Q on the incident wavefront. Suppose that when disturbance from point P, the disturbance from point Q reaches Q' via kpoint k on the surface. The time taken by light to travel from any point on incident wavefront to the corresponding point on the reflected wave front should always be same. Let C is velocity of light then taken by light to go from Q to Q' is given by

In right angle ΔAQK, ∠PAP' = i, Therefore,OK = AK sin i and in right angled ΔKQ'P', ∠A'P; A = r Therefore, KQ' = KP sinr
Substituting the value of QK and KQ' in equation (i), we have

For rays from different points on incident wave front, the values of AK are different. The rays from different points on incident wave front takes same time to reach corresponding points on the reflected wave front, it , given by the above euqation (ii) is independent of AK.
It will.happen so, AK (sin i - sin r) = 0
or, Sin i = Sin r
or, i = r
i.e. angle of incidence is equal to the angle of reflection.
Further, as the incident wave front (PA), the reflecting surface(XY) and the reflected wave front (P'A') are all perpendicular to the plane of the paper, therefore, the incident ray (LA or MP') normal (AN) and the reflected ray (AA'L' or P'M'), which are respectively perpendicular to AP, XY and A'P" all lie in the same plane. Hence, the laws by reflection are proved on the basis of wave theory.
Verification of refraction on the basis of wave theory of Huygen's principle:
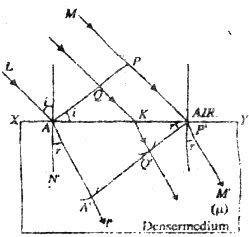
Let XY be a plane surface separating air from a denser medium and PA and MP to the incident wave front represent incident rays. Let AN is normal to the surface at point A, then LNAL = i is the angle of incidence. First of all the wave front reaches point A. From the points located between A to P, the wavefront reaches points between A to P, later in time but in the same order, so that it reaches point P'; in the last. Thus different points on the surface XY becomes source of secondary wavelets at different instants of time. When the disturbance from point P on incident wave front reaches point P' on the surface XY, the secondary wavelet from point A on the surface will have grown into a sphere inside the denser medium of radius AA'.
Such that

where v is the velocity of light in denser medium and c is the velocity of light in air.
Draw a circle of radius A'A = v/c x PP'
From point P', draw a tangent tangent Plane P'A' sphere. Then P'A' represents refracted wavefront and lines AA 'L' and P'M' to the refracted wavefront refractive rays. Also LN'AA = r is the angle of refraction.
Consider any point Q on the incident wave front. Suppose that when disturbance from'point P on incident wavefront reaches point P'on refracted wavefront, the disturbance from point q reaches point Q' via point K on the surface of separation of air and densr medium. Since P'A'represents the refracted wavefront, the time taken by light to travel from a point on incident wavefront to the corresponding point on refracted wavelength should be constant. Now, time taken by light to go from Q to Q' si given by

In right angle ΔAQK, ∠ZOAK = i, Therefore QK = AK sin i and in right angled ΔP'Q'K, ZQ'P'K = r. Therefore, KQ - Kp' sin r.
Substituting the value for QK and KQ' in equation (iii), we have

For rays from different points on the incident wave front, the values of AK are different. The rays from different points on incident wave front will take same time to reach corresponding points on the refracted wave front, if r given by equation (iv) is independent of AK. It will happen so, if

But μ is constant and is called the refractive index of the denser medium with respect to air.
