A 4 x 4 determinant can be expanded in terms of 3 by 3 determinants called minors. Let's take an example
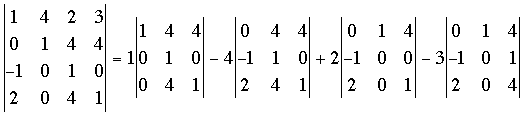
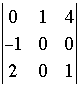
Here I have expressed the 4 by 4 determinant in terms of 4, 3 by 3 determinants. To see what I did look at the first row of the 4 by 4 determinant. This row is 1, 4, 2, 3. These are the coefficients of the 3 by 3 determinants but with alternating signs, that is 1, -4, 2, -3. Each of these coefficients is multiplied by the 3 by 3 determinant obtained by removing the row and column of the 4 by 4 determinant that contains this coefficient. For example looking at the 2 in the first row of the 4 by 4 determinant, the minor obtained by removing the first row and third column is
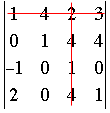
or