Consider A = {-1, 1, 2, 3} and B = {1, 4, 9}
It is given that f: A → B: f(x) = x2 Ɐ x ∈ A
Each element in A has unique image in B where f is a function from A to B
By substituting the values
f(-1) = (-1)2 = 1
f(1) = 12 = 1
f(2) = 22 = 4
f(3) = 32 = 9
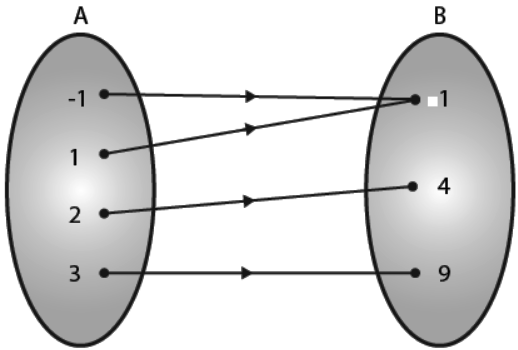
Here, two elements -1 and 1 have same image 1 ∈ B
Hence, f is many-one.