If two points on a given line subtend equal angles at two distinct points which lie on the same side of the line, then the four points are

Question

Theorem :  If two points on a given line subtend equal angles at two distinct points which lie on the same side of the line, then the four points are concyclic.  

Answer 1

Given: Points B and C lie on the same side of the line AD ∠ABD = ∠ACD 

To prove: Points A, B, C, D are concyclic. 

i.e., □ABCD is a cyclic quadrilateral.

Proof: 

Suppose points A, B, C, D are not concyclic points.

We can still draw a circle passing through three non collinear points A, B, D. 

Case I: Point C lies outside the circle. Then, take point E on the circle such that A – E – C. 

∠ABD ≅ ∠AED (i) [Angles inscribed in the same arc] 

∠ABD ≅ ∠ACD (ii) [Given] 

∴ ∠AED ≅ ∠ACD [From (i) and (ii)]

∴ ∠AED ≅ ∠ECD [A – E – C]

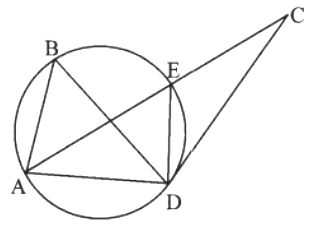
But, ∠AED ≅ ∠ECD as ∠AED is the exterior angle of ∆ECD. 

∴ Our supposition is wrong. 

∴ Points A, B, C, D are concyclic points. 

Case II: Point C lies inside the circle. Then, take point E on the circle such that A – C – E. 

∠ABD ≅ ∠AED (iii) [Angles inscribed in the same arc] 

∠ABD ≅ ∠ACD (iv) [Given] 

∴ ∠AED ≅ ∠ACD [From (iii) and (iv)] 

∴ ∠CED ≅ ∠ACD [A – C – E]

But, ∠CED ≅ ∠ACD as ∠ACD is the exterior angle of ∆ECD. 

∴ Our supposition is wrong. 

∴ Points A, B, C, D are concyclic points.