Question

Explain displacement in S.H.M. Find the relations between them.

Answer 1

Displacement: Consider a reference particle moving on a circle of reference of radius a with uniform angular velocity ω. Let the particle start from the point X and trace angular distance θ radian in time t as it reaches the point P.

Therefore, ω = \(\frac{\theta}{t}\) or θ = ωt.

Let the projection of the particle P on diameter YOY’ be at M. Then OM = y is the displacement in S.H.M. at time t.

In ∆OPM, sin θ = \(\frac{OM}{OP}\) = \(\frac{y}{a}\)

or  y = a sin θ = a sin ωt …(i)

Important notes.

(i) If projection of P is taken on diameter XOX’, then point N will be executing S.H.M. Here, ON = x = Displacement in S.H.M. at time t.

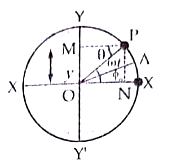
In ∆ONP, cos θ = \(\frac{ON}{OP}\) 

or x = a cos θ = a cos ωt …(ii)

(ii) If A is the starting position of the particle of reference such that ∠AOX = ϕ₀ and ∠XOP = ωt.

Θ = ∠XOA = ωt − ϕ₀

Here (−) ϕ₀ is called the initial phase or epoch of S.H.M.

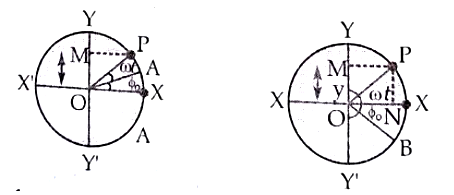
(iii) If B is the starting position of the particle of reference such that

∠BOX = ϕ₀

∠BOP = ωt.

Θ = ∠XOP = ωt + ϕ₀

From equation (i) y = a sin(ωt + φ₀)

From equation (ii) x = a cos(ωt + ϕ₀ )

Here (+) ϕ₀ is called initial phase or epoch of S.H.M.