Find dy/dx of the following 1. y = (logx)^cosx 2. x = 2at^2, y = at^4

Question

Find \(\frac{dy}{dx}\) of the following

1. y = (logx)^cosx
2. x = 2at², y = at⁴
3. x = a(cosθ + θsinθ), y = a(sinθ – θcosθ)
4. y=x^x
5. y =(x log x)^log(logx)
6. \(\sqrt{sinx{\sqrt{sinx+{\sqrt{sinx+....}}}}}\)
7. y^x = x^siny
8. y =(log x)^x + x^logx
9. y = (sinx)^x + sin^-1\(\sqrt{x}\)

Answer 1

1. Given; 

y = (logx)^cosx, taking log on both sides;
log y = cosxlog(logx),
Differentiating with respect to x;

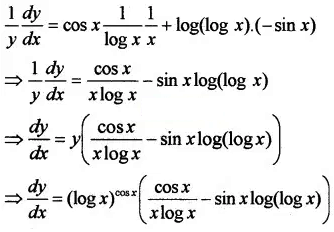
2. Given; x = 2at² ⇒ \(\frac{dx}{dt}\) = 4at

3. Given; 

x = a(cosθ + θsinθ)
\(\frac{dx}{dθ}\) = a(-sinθ + θcosθ + sinθ) = aθcosθ
y = a(sinθ – θcosθ)
\(\frac{dx}{dθ}\) = a(cosθ – θ(-sinθ) – cosθ) = aθ sinθ
\(\frac{dx}{dθ}\) = \(\frac{aθsinθ​​}{aθcosθ}\)= tanθ

4. y= x^x; Taking log on both sides;
log y = x log x

5. y = (x log x)^{log logx}
Taking log on both sides;
log y = (log log x) [log (xlogx)]

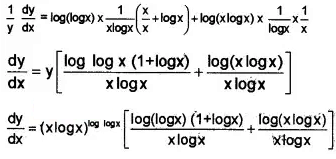
6. \(y = \sqrt{sinx + y}\) ⇒ y² = sinx + y

⇒ y² – y = sinx

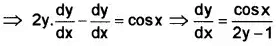
7.  y^x = x^{sin y};
Taking log on both sides;
xlogy = siny log x

8. y = (log x)^x + x^logx = u + v

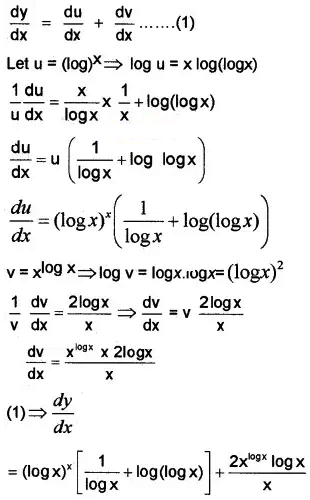
9. y = (sinx)^x + sin^{-1\(\sqrt{x}\)}
Let u = (sinx)^x ⇒ log u = x log sinx