Question

Prove that every square matrix can be uniquely expressed as the sum of a symmetric matrix and skew-symmetric matrix.

Answer 1

Let A be any square matrix.

Then,

∴ P is symmetric matrix.

Also,

∴ Q is skew - symmetric matrix.

Thus, A = P + Q, 

Where P is a symmetric matrix and  Q is a skew-symmetric matrix.

Hence, A is expressible as the sum of a symmetric and a skew-symmetric matrix.

Uniqueness : If possible,

Let A = R + S,

Where R is symmetric and S is skew-symmetric, then,

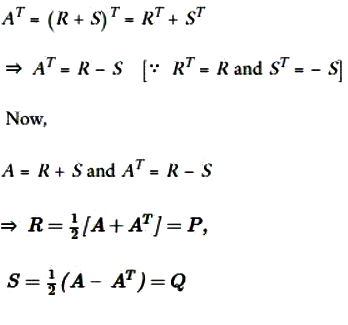
Hence, A is uniquely expressible as the sum of a symmetric and a skew-symmetric matrix.