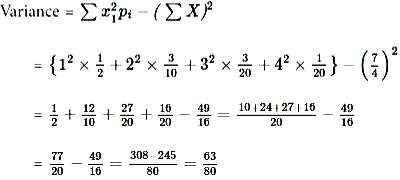First six positive integers are 1,2,3,4,5 and 6.
If three numbers are selected at random from above six numbers then the numbers of elements in sample space S is given by
i.e., 
Here X, smallest of the three numbers obtained, is random variable X may have value 1,2,3 and 4.
Therefore, required probability distribution is given as
P(X = 1) = Probability of event getting 1 as smallest number
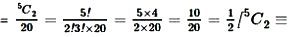
selection of two numbers out if 2,3,4,5,6]
P(X = 2) = Probability of events getting 2 as smallest number.


P(X = 3) = Probability of events getting 3 as smallest number.

P(X = 4) = Probability of events getting 4 as smallest number.

Required probability distribution table is
| X or xi |
1 |
2 |
3 |
4 |
| P(X) or pi |
\(\frac{1}{2}\) |
\(\frac{3}{10}\) |
\(\frac{3}{20}\) |
\(\frac{1}{20}\) |