Question

Find the area of the region {(x, y) : x ≤ y ≤ |x|}.

Answer 1

Given curves are

x² + y² = 16.....(i)

y² = 6x.....(ii)

Obviously curve (i) is a circle having centre at (0, 0) and radius 4 unit.

While curve (ii) is right handed parabola having vertex at (0, 0) and axis along +ve direction of x-axis.

Required part in the shaded region.

Now, for intersection point of curve (i) & (ii)

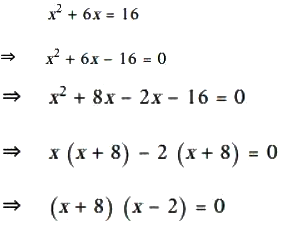
⇒ x = -8 or 2 

 [\(\therefore\) x = -8 is not possible as y² is +ve]

\(\therefore\) x = 2
\(\therefore\) y = \(\pm\sqrt{12}\) = \(\pm2\sqrt{3}\)

Hence, coordinate of B is (2, 2√3).

Since, shaded region i.e., required part is symmetrical about x-axis.

Therefore, area of required part

= 2 [Area OBEDO]

= 2 [Area DEBFD - Area OBFO]