To find weather the function f(x) is derivable at a point x = c we have to check that
f ‘(c -) = f ‘(c +) = finite quantity, this condition must be fulfilled in order the function to be derivable.
As discussed above the top of this document where description of the topic is given.
The given function is,
f (x) = │sin x│,
To find weather the function is derivable or not we can either make graph of the function and look for pointed edges, not smooth edges, where there are multiple slopes present which makes the function non derivable.
The graph of the function sin x is,

The graph of │sin x│ is,

As you can see at every integral multiple of π there is a pointed turn which shows multiple slopes at one point which makes the function non derivable.
We can also solve the problem by algebraic method, which is,

this is the resolved function with which we can solve by using limits method.
f (x) = cos│x│,
To find weather the function is derivable or not we can either make graph of the function and look for pointed edges, not smooth edges, where there are multiple slopes present which makes the function non derivable.
The graph of the cos x is,
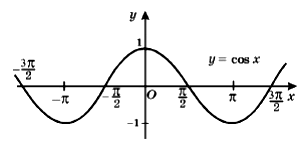
As we know the property of cos x which is cos(- x) = cos x which means that weather there is modulus with the angle of cose or not there is no difference.
Hence the curve do not have any sharp points, so it is derivable hence cos x is differentiable everywhere so │cos x│ is also differentiable everywhere.
We can also prove by algebraic method by taking a general angle ‘x’ and prove for it.