Prove that the semi - vertical angle of the right circular cone of given volume and least curved surface is cot^(-1)(√2). ​

Question

Prove that the semi - vertical angle of the right circular cone of given volume and least curved surface is cot^-1(\(\sqrt2\)).

Answer 1

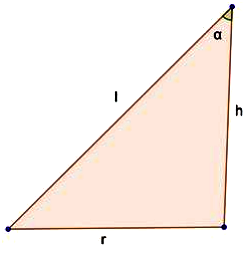
Let ‘r’ be the radius of the base circle of the cone and ‘l’ be the slant length and ‘h’ be the height of the cone : 

Let us assume ‘α’ be the semi - vertical angle of the cone.

We know that Volume of a right circular cone is given by :

⇒ V = \(\frac{\pi r^2h}{3}\)

Let us assume r²h = k(constant) …… (1)

⇒ V = \(\frac{\pi k}{3}\)

⇒ h = \(\frac{k}{r^2}\) ...(2)

We know that surface area of a cone is,

⇒ S = πrl …… (3)

From the cross - section of cone we see that,

⇒ I² = r² + h² ...(4)

Substituting (4) in (3), we get

⇒ S = πr(\(\sqrt{(r^2+h^2)}\)

From (2),

Let us consider S as a function of R and We find the value of ‘r’ for its extremum, 

Differentiating S w.r.t r we get,

⇒ \(\frac{dS}{dr}\) = \(\frac{d}{dr}(\frac{\pi\sqrt{r^6+k^2}}{r})\)

Differentiating using U/V rule,

Equating the differentiate to zero to get the relation between h and r.

Since the remainder is greater than zero only the remainder gets equal to zero 

⇒ 2r⁶ = k² 

From(1) 

⇒ 2r⁶ = (r²h)² 

⇒ 2r⁶ = r⁴h² 

⇒ 2r² = h² 

Since height and radius cannot be negative,

⇒ h = \(\sqrt2\)r …… (5)

From the figure,

⇒ cot α = \(\frac{h}{r}\)

From(5)

⇒ cot α = \(\sqrt2\)

⇒ α = cot^-1\(\sqrt2\)

∴ Thus proved.