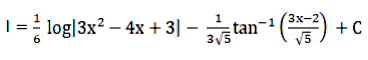Evaluate the integral : ∫(x-1)/(3x^2-4x+3)dx ​

Question

Evaluate the integral :

\(\int\frac{x-1}{3x^2-4x+3}\)dx

Answer 1

I = \(\int\frac{x-1}{3x^2-4x+3}\)dx

As we can see that there is a term of x in numerator and derivative of x² is also 2x..

So there is a chance that we can make substitution for 3x² –4x + 3 and I can be reduced to a fundamental integration.

As, 

∴ Let, x – 1 = A(6x – 4) + B 

⇒ x – 1 = 6Ax – 4A + B 

On comparing both sides – 

We have, 

6A = 1 

⇒ A = 1/6 –4A + B = –1 

⇒ B = –1+4A = –2/6 = –1/3 

Hence,

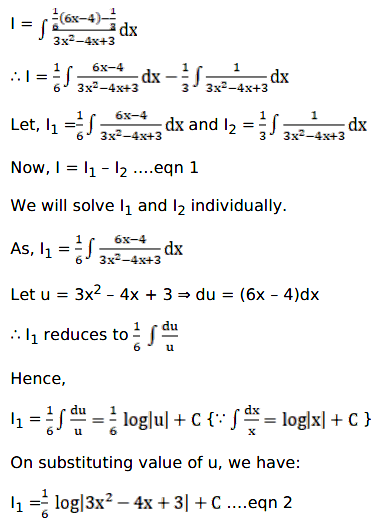
As,

 I₂ = \(\frac{1}{3}\int\frac{1}{3x^2-4x+3}\) and we don’t have any derivative of function present in denominator. 

∴ we will use some special integrals to solve the problem.

As denominator doesn’t have any square root term. 

So one of the following two integrals will solve the problem.

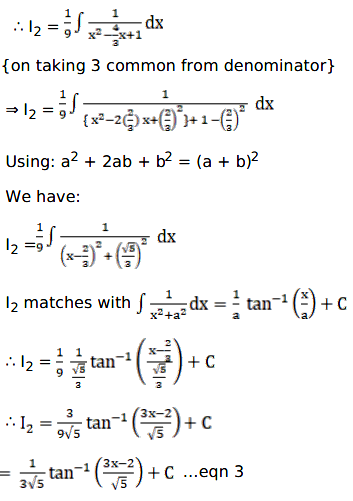
From eqn 1: 

I = I₁ – I₂ 

Using eqn 2 and eqn 3 :