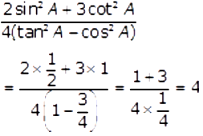If cosecA = √2, find the value of 2sin^2A + 3cot^2A/4(tan^2A - cos^2A)

Question

If cosecA = √2, find the value of \(\frac{2sin^2A + 3cot^2A}{4(tan^2A - cos^2A)}\)

Answer 1

Given, cosecA = √2

⇒ Cot²A = cosec²A - 1 = (√2)² - 1

= 2 - 1 = 1

and, tan² A = \(\frac{1}{cot^2A}\) = \(\frac{1}{1}\) = 1

⇒ sin²A = \(\frac{1}{cosec^2A}\) = \(\frac{1}{\Big(\sqrt{2}\Big)^2}\) = \(\frac{1}{2}\) 

⇒ cos²A = 1 - sin² A = 1 - \(\Big(\frac{1}{2}\Big)^2\) = 1 - \(\frac{1}{4}=\frac{3}{4}\) 

Now,