Solution of the differential equation dy/dx + y/x = sin x is

Question

Solution of the differential equation \(\frac{dy}{dx}+\frac{y}{x}=sin\,x\) is

A. x (y + cos x)= sin x + C

B. x (y – cos x)= sin x + C

C. x (y + cos x)= cos x + C

D. None of these

Answer 1

Correct answer is A.

dy/dx + y/x = sin x

Since it is a form of linear differential equation.

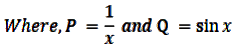
Integrating Factor (I.F) = e∫ p dx

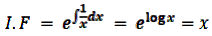
Solution of differential equation is given by

y.(I.F) = ∫ Q.(I.F) dx + C

⇒ y. x = ∫ (sin x).x dx + C

⇒ y. x = ∫ (sin x).x dx + C

Consider integral ∫ (sin x).x dx

Treating x as first function and sin x as second function. So, integrating by Parts we get,

⇒ x. (-cos x) + ∫ 1.cos x dx + C

⇒ – x. cos x + sin x + C

∴ y. x = – x. cos x + sin x + C

⇒ x (y + cos x) = sin x + C is the required solution.