Question

Find a unit vector perpendicular to both the vectors 4i - j + 3k and  -2i + j - 2k.

Answer 1

Given two vectors \(4\hat i-\hat j + 3\hat k\) and  \(-2\hat i+\hat j-2\hat k\)

Let  \(\vec a=4\hat i-\hat j+3\hat k\) and \(\vec b=-2\hat i + \hat j-2\hat k\)

We need to find a unit vector perpendicular to  \(\vec a\) and  \(\vec b\).

Recall a vector that is perpendicular to two vectors

Here, we have (a₁, a₂, a₃) = (4, –1, 3) and (b₁, b₂, b₃) = (–2, 1, –2)

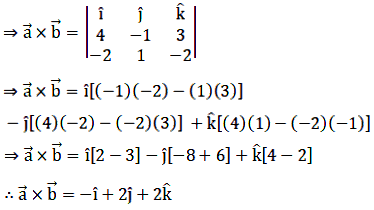
Let the unit vector in the direction of  \(\vec a\times\vec b\) be \(\hat p\).

We know unit vector in the direction of a vector  \(\vec a\) is given by  \(\hat a=\cfrac{\vec a}{|\vec a|}\).

Recall the magnitude of the vector  \(\text x\hat i+y\hat j+z\hat k\)  is

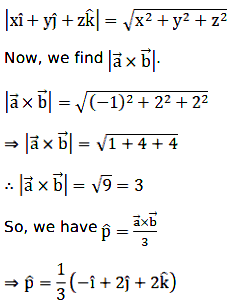
Thus, the required unit vector that is perpendicular to both  \(\vec a\) and  \(\vec b\) is  \(\cfrac13(-\hat i+2\hat j+2\hat k)\).