Question

A circular track of radius 300m is kept with outside of track raised to make 5 degree with the horizontal.

1. Name the process in which outside of the road is raised little above the inner.

2. Obtain an expression for the optimum speed to avoid skidding (considering to friction)

Answer 1

1. Banking of roqd

2. 

Consider a vehicle along a curved road with angle of banking θ. Then the normal reaction on the ground will be inclined at an angle θ with the vertical.

The vertical component can be divided into N Cosθ (vertical component) and N sinθ (horizontal component). The frictional force can be divided into two components. Fcosθ (horizontal component) and F sinθ (vertical component).

From the figure

N cos θ = F sinθ + mg

N cosθ – F sinθ = mg ______(1)

The component Nsin0 and Fsinθ provide centripetal force. Hence

N sinθ + F cos θ = \(\frac{mv^2}{R}\) ______(2)

eq (1) by eq (2)

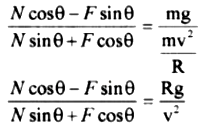
Dividing both numerator and denominator of L.H.S by N cosθ. We get

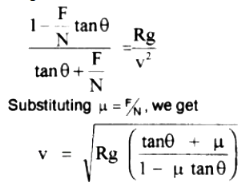
This is the maximum speed at which vehicle can move over a banked curved road.

Optimum speed:

Optimum speed is the speed at which a vehicle can move over a curved banked road without using unnecessary friction. 

Putting µ = 0 in the above equation we get

v₀ = \(\sqrt{Rgtanθ}\).