Question

Find the direction cosines of the unit vector perpendicular to the plane r.(6i - 3j - 2k) + 1 = 0 passing through the origin.

Answer 1

The given plane equation is

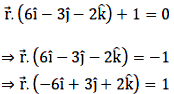
Now, we calculate the magnitude of the vector \(-6\hat i+3\hat j+2\hat k.\)

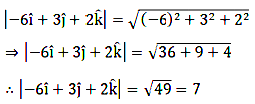
On dividing both sides of the plane equation by 7, we get

Recall that the equation of the plane in normal form is given by  \(\vec r.\hat n=d\) where \(\hat n\) is a unit vector perpendicular to the plane through the origin.

So, here

This is a unit vector normal to the plane  \(\vec r.(6\hat i-3\hat j-2\hat k)+1=0.\)

Thus, the direction cosines of the unit vector perpendicular to the given plane are