Given:
⇒ Bag A contains 4 red balls and 5 black balls
⇒ Bag B contains 3 red balls and 7 black balls
It is told that one ball is drawn is drawn from is each bag.
We need to find the probability that the balls are of same colour.
Let us find the Probability of drawing each colour ball from the bag.
⇒ P(B1) = P(drawing black ball from bag A)


We need to find the probability of drawing the different colour balls from two bags
⇒ P(DRB) = P(drawing one red ball and one Black ball)
⇒ P(DRB) = P(drawing black balls from bag A and red ball from bag B) + P(drawing black balls from bag B and red ball from bag A)
Since drawing a ball is independent for each bag, the probabilities multiply each other.
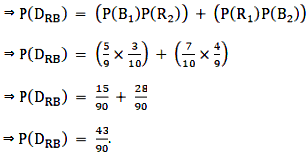
We need to find the probability of drawing the same colour balls from two bags
⇒ P(S) = P(drawing two balls of same colours) = P(drawing black balls from each bag) + (P(drawing white balls from each bag)
Since drawing a ball is independent for each bag, the probabilities multiply each other.

∴ The required probabilities are \(\cfrac{43}{90},\cfrac{47}{90}.\)