Coloured balls are distributed in four boxes as shown in the following table: box ( I ,II, III, IV) colour (black, white, red, blue)

Question

Coloured balls are distributed in four boxes as shown in the following table: 

Box	Colour
	Black	White	Red	Blue
I	3	4	5	6
II	2	2	2	2
III	1	2	3	1
IV	4	3	1	5

A box is selected at random and then a ball is randomly drawn from the selected box. The colour of the ball is black, what is the probability that ball drawn is from the box III.

Answer 1

Given:

Box I has 3 Black, 4 White, 5 Red, 6 Blue balls

Box II has 2 Black, 2 White, 2 Red, 2 Blue balls

Box III has 1 Black, 2 White, 3 Red, 1 Blue balls

Box IV has 4 Black, 3 White, 1 Red, 5 Blue balls

Let us assume U₁, U₂, U₃, U₄ and A be the events as follows:

U₁ = choosing Box I

U₂ = choosing Box II

U₃ = choosing Box III

U₄ = choosing Box IV

A = choosing Black ball from box We know that each urn is most likely to choose. So, probability of choosing a urn will be same for every Urn

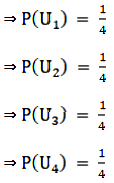
The Probability of choosing balls from each box differs from box to box and the probabilities are as follows:

⇒ P(A|U₁) = P(Choosing black ball from Box I)

⇒ P(A|U₃) = P(Choosing black ball from Box III)

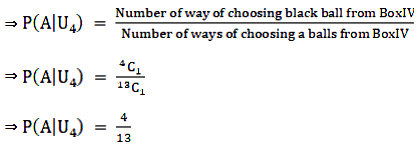
Now we find

P(U₃|A) = P(The black ball is from Ball III)

Using Baye’s theorem:

∴ The required probability is \(\cfrac{156}{947}.\)