Prove the following identities 1-((sin^2x)/(1 + cot x)) - ((cos^2x)/(1 + tan x)) = sin x cos x

Question

Prove the following identities

\(1-\cfrac{sin^2\text x}{1+cot\,\text x}-\cfrac{cos^2\text x}{1+tan\,\text x}\) = sin x cos x

Answer 1

LHS = \(1-\cfrac{sin^2\text x}{1+cot\,\text x}-\cfrac{cos^2\text x}{1+tan\,\text x}\)

We know that  tan θ = \(\cfrac{sin\,\theta}{cos\,\theta}\) and cot θ = \(\cfrac{cos\,\theta}{sin\,\theta}\)

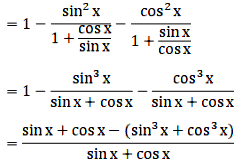
We know that a³ + b³ = (a + b) (a² + b²- ab)

= 1 – (sin²x + cos²x) + sinx cosx

We know that sin²x + cos²x = 1.

= 1 – 1 + sinx cosx

= sinx cosx

= RHS

Hence proved.