The shape of a toy is given as f(x) = 6(2x^4 – x^2 ). To make the toy beautiful 2 sticks

Question

1. Which value from the following may be abscissa of critical point?

a. ± \(\cfrac14\)

b. ± \(\cfrac12\)

c. ± 1

d. None

2. Find the slope of the normal based on the position of the stick

 a. 360

b. –360

c. \(\cfrac1{360}\)

d. \(\cfrac{-1}{360}\)

3. What will be the equation of the tangent at the critical point if it passes through (2, 3)?

a. x + 360y = 1082

b. y = 360x – 717

c. x = 717y + 360

d. none

4. Find the second order derivative of the function at x = 5.

a. 598

b. 1176

c. 3588

d. 3312

5. At which of the following intervals will f(x) be increasing?

a. (-∞, -1/2) ꓴ (1/2, ∞)

b. (-1/2, 0) ꓴ (1/2, ∞)

c. (0, ½) ꓴ (1/2, ∞)

d. (-∞, -1/2) ꓴ (0, ½)

Answer 1

1. b) ± \(\cfrac12\)

2. d) \(\cfrac{-1}{360}\)

3. b) y = 360x  – 717

4. c) 3588

5. b) (-1/2, 0) ꓴ (1/2, ∞)

Answer 2

1. (b) \(\pm \frac 12\)

Critical point is point where f'(x) = 0

f(x) = 6(2x⁴ - x²)

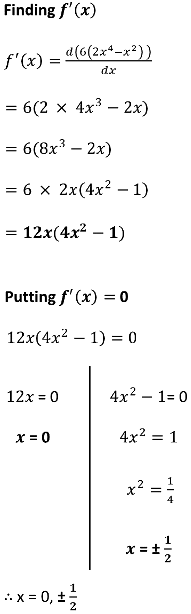
2. (d) \(\frac{-1}{360}\)

We need to find Slope of Normal at (2, 3)

First, let's find Slope of Tangent at (2, 3)

Slope of tangent = f'(x) 

= 12x(4x² - 1)

Putting x = 2

= 12 x 2 x (4(2)² - 1)

= 24(4 x 4 -1)

= 24(16 - 1)

= 24 x 15

= 360

Thus,

Slope of Normal = -1/Slope of Tangent

= \(\frac{-1}{360}\)

3 . (b) y = 360x - 717

We found the slope of tangent at (2, 3)

Slope of tangent at (2, 3) = 360

Finding equation of line passing through (2, 3) with slope 360

y - y₁= Slope(x - x₁)

y - 3 = 360(x - 2)

y - 3 = 360x - 720

y = 360x - 720 + 3

y = 360x - 717

4. (c) 3588

We know that

f(x) = 6(2x⁴ - x²)

And,

f'(x) = 12x(4x² - 1)

= 48x³ - 12x

Now,

\(f''(x) = \frac{d(48x^3 - 12x)}{dx}\)

\(= 48 \times 3x^2 - 12\)

= 144x² - 12

Putting x = 5

= 144 x 5² - 12

= 144 x 25 - 12

= 3600 - 12

= 3588

5. (b) \((\frac 12, 0) \cup (\frac 12, \infty)\)

f(x) is increasing where f'(x) > 0

Hence,

\(\therefore\) f is strictly increasing in \((\frac 12, 0) \) and \( (\frac 12, \infty)\).