Question

Solve the following quadratics x² – 4x + 7 = 0

Answer 1

Given x² – 4x + 7 = 0 

⇒ x² – 4x + 4 + 3 = 0 

⇒ x² – 2(x)(2) + 2² + 3 = 0 

⇒ (x – 2)² + 3 = 0 [∵ (a – b)² = a² – 2ab + b²] 

⇒ (x – 2)² + 3 × 1 = 0 

We have i² = –1 

⇒ 1 = –i² 

By substituting 1 = –i² in the above equation, we get 

(x – 2)² + 3(–i²) = 0 

⇒ (x – 2)² – 3i² = 0

⇒ (x – 2)² - \((\sqrt{3}i)^2\) = 0

Since a² – b² = (a + b)(a – b), we get

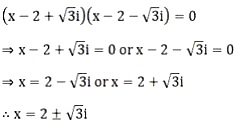
Thus, the roots of the given equation are 2 ± \(\sqrt{3}\) i.​​​​​​