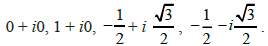Question

Solve the equation z² = z , where z = x + iy

Answer 1

z² = z ⇒ x² – y² + i2xy = x – iy

Therefore, x² – y² = x  ...(1) and

2xy = – y       ... (2)

From (2), we have y = 0 or x = -1/2

When y = 0, from (1), we get x² – x = 0, i.e., x = 0 or x = 1.

When x =-1/2, from (1), we get y² = 1/4 +1/2 or y² =3/4, i.e., y =±√3/2

Hence, the solutions of the given equation are